A Synthèse des liens entre les différentes méthodes de construction de moyennes mobiles

Cette annexe montre comment tous les filtres étudiés peuvent se retrouver à partir d’une formule générale de construction des moyennes mobiles. Elle décrit également les relations d’équivalences entre les différentes méthodes. Enfin, des graphiques synthétiques résument ces propriétés.

A.1 Formule générale de construction des filtres

Pour établir une formule générale englobant les principaux filtres linéaires, Grun-Rehomme, Guggemos, et Ladiray (2018) définissent deux critères. En changeant légèrement les notations utilisées par les auteurs afin d’avoir une formulation plus générale, ces deux critères peuvent s’écrire : \[\begin{align} I(\boldsymbol\theta,q,y_t,u_t)&=\E{(\Delta^{q}(M_{\boldsymbol\theta} y_t-u_t))^{2}} \tag{15} \\ J(\boldsymbol\theta,f, \omega_1,\omega_2)&=\int_{\omega_1}^{\omega_2} f\left[\rho_{\boldsymbol\theta}(\omega), \varphi_{\boldsymbol\theta} (\omega), \omega\right] \ud \omega \tag{16} \end{align}\] où $y_t$ est la série étudiée, $u_t$ une série de référence³⁵ et $\Delta$ est l’opérateur différence ($\Delta y_t=y_t-y_{t-1}$ et $\Delta^q=\underbrace{\Delta \circ \dots \circ \Delta}_{q\text{ fois}}$ pour $q\in\N$). Dans la majorité des cas, la fonction $f$ ne dépendra que de la fonction de gain, $\rho_{\boldsymbol\theta}$, et de la fonction de déphasage, $\varphi_{\boldsymbol\theta}$. Dans ce cas, par simplification on écrira $f\left[\rho_{\boldsymbol\theta}(\omega), \varphi_{\boldsymbol\theta} (\omega), \omega\right] = f\left[\rho_{\boldsymbol\theta}(\omega), \varphi_{\boldsymbol\theta} (\omega)\right]$.

La majorité des filtres linéaires peut s’obtenir par une minimisation d’une somme pondérée de ces critères, sous contrainte linéaire sur les coefficients : \[ \begin{cases} \underset{\boldsymbol\theta}{\min} & \sum_i \alpha_i I(\boldsymbol\theta,\, q_i,\, y_t,\, u_t^{(i)})+ \beta_iJ(\boldsymbol\theta,\, f_i,\, \omega_{1,i},\, \omega_{2,i})\\ s.t. & \boldsymbol C\boldsymbol \theta=\boldsymbol a \end{cases} \]

En effet :

L’extension des méthodes polynomiales de Proietti et Luati (2008) présentée dans la section 2.3 revient en effet à minimiser une somme pondérée de l’erreur quadratique de révision : \[ \E{\left( \sum_{i=-h}^h\theta^s_{i}y_{t+s}-\sum_{i=-h}^qv_iy_{t+s} \right)^2} = I(v,\,0,\,y_t,\,M_{\boldsymbol \theta^s} y_t), \] et du critère de timeliness : \[ T_g(\boldsymbol\theta) = J(f\colon(\rho,\varphi)\mapsto\rho^2\sin(\varphi)^2,\,\omega_1, \,\omega_2). \] sous une contrainte linéaire.
Les critères des filtres symétriques de Gray et Thomson (1996) (section 2.4) sont : \[\begin{align*} F_{GT}(\boldsymbol\theta)&=I(\boldsymbol\theta,0,y_t,g_t),\\ S_{GT}(\boldsymbol\theta)&=I(\boldsymbol\theta,d+1,y_t,0). \end{align*}\] Les filtres asymétriques sont construits en minimisant l’erreur quadratique moyenne des révisions sous contraintes linéaires (préservation d’un polynôme de degré $p$).
Les trois critères de la méthode FST de Grun-Rehomme, Guggemos, et Ladiray (2018) se retrouvent en notant $y_t=TC_t+\varepsilon_t,\quad\varepsilon_t\sim\Norm(0,\sigma^2)$ avec $TC_t$ une tendance déterministe : \[\begin{align*} F_g(\boldsymbol\theta) & = I(\boldsymbol\theta,\,0,\,y_t,\,\E{M_{\boldsymbol\theta} y_t})\\ S_g(\boldsymbol\theta) & = I(\boldsymbol\theta,\,q,\,y_t,\,\E{M_{\boldsymbol\theta} y_t})\\ T_g(\boldsymbol\theta) & = J(f\colon(\rho,\varphi)\mapsto\rho^2\sin(\varphi)^2,\,\omega_1, \,\omega_2). \end{align*}\]
Les quatre critères $A_w$, $T_w$, $S_w$ et $R_w$ des filtres de Wildi et McElroy (2019) sont des cas particuliers du critère $J$ défini dans l’équation (15). En notant : \[ \begin{cases} f_1\colon&(\rho,\varphi, \omega)\mapsto2\left(\rho_s(\omega)-\rho\right)^{2}h(\omega) \\ f_2\colon&(\rho,\varphi, \omega)\mapsto8\rho_s(\omega)\rho\sin^{2}\left(\frac{\varphi}{2}\right)h(\omega) \end{cases}, \] on a : \[\begin{align*} A_w(\boldsymbol\theta)&= J(\boldsymbol\theta,f_1,0,\omega_1),\\ T_w(\boldsymbol\theta)&= J(\boldsymbol\theta,f_2,0,\omega_1),\\ S_w(\boldsymbol\theta)&= J(\boldsymbol\theta,f_1,\omega_1,\pi),\\ R_w(\boldsymbol\theta)&= J(\boldsymbol\theta,f_2,\omega_1,\pi). \end{align*}\]
Les filtres des espaces de Hilbert à noyau reproduisant correspondent à une sélection optimale du paramètre $b$ selon les critères précédents, en imposant comme contrainte linéaire que les coefficients soient sous la forme $w_j=\frac{K_{d+1}(j/b)}{\sum_{i=-h}^{^p}K_{d+1}(i/b)}$.

A.2 Liens entre les différentes méthodes

A.2.1 Critères de Gray et Thomson et ceux de Grun-Rehomme et alii

Les critères $F_g$ et $S_g$ peuvent se déduire de $F_{GT}$ et $S_{GT}$. Les approches de Gray et Thomson (1996) et Grun-Rehomme, Guggemos, et Ladiray (2018) sont donc équivalentes pour la construction de filtres symétriques.

Notons $\boldsymbol x_{t}=\begin{pmatrix}1 & t & t^{2} & \cdots & t^{d}\end{pmatrix}'$, $\boldsymbol \beta=\begin{pmatrix}\beta_{0} & \cdots & \beta_{d}\end{pmatrix}'$.

Pour le critère de fidelity : \[ \hat{g}_{t}-g_{t}=\left(\sum_{j=-h}^{+h}\theta_{j}\boldsymbol x_{t+j}-\boldsymbol x_{t}\right)\boldsymbol \beta+\sum_{j=-h}^{+h}\theta_{j}\varepsilon_{t+j}+\sum_{j=-h}^{+h}\theta_{j}(\xi_{t+j}-\xi_{t}), \] Si $\theta$ préserve les polynômes de degré $d$ alors $\sum_{j=-h}^{+h}\theta_{j}\boldsymbol x_{t+j}=\boldsymbol x_{t}$. Puis, comme $\xi_{t}$ et $\varepsilon_{t}$ sont de moyenne nulle et sont non corrélés : \[ F_{GT}(\boldsymbol\theta)=\E{(\hat{g}_{t}-g_{t})^{2}}=\boldsymbol \theta^{'}\left(\sigma^{2}\boldsymbol I+\boldsymbol \Omega\right)\boldsymbol \theta. \] Si $\xi_t=0$ alors $\boldsymbol \Omega=0$ et $F_{GT}(\boldsymbol\theta)=F_g(\boldsymbol\theta)$.

Pour la smoothness on a : \[ \nabla^{q}\hat{g}_{t}=\sum_{j=h}^{h}\theta_{j}\underbrace{\nabla^{q}\left(\left(x_{j}-x_{0}\right)\beta\right)}_{=0\text{ si }q\geq d+1}+\sum_{j=h}^{h}\theta_{j}\nabla^{q}\varepsilon_{t+j}+\sum_{j=h}^{h}\theta_{j}\nabla^{q}\xi_{t+j}. \] D’où pour $q=d+1$ : \[ S_{GT}(\boldsymbol\theta)=\E{(\nabla^{q}\hat{g}_{t})^{2}}=\boldsymbol \theta^{'}\left(\sigma^{2}\boldsymbol B_{q}+\boldsymbol \Gamma_{q}\right)\theta. \] On peut, par ailleurs, montrer que pour toute série temporelle $X_t$, \[ \nabla^{q}(M_{\boldsymbol\theta}X_{t})=\left(-1\right)^{q}\sum_{k\in\Z}\left(\nabla^{q}\theta_{k}\right)X_{t+k-q}, \] avec $\theta_k=0$ pour $|k|\geq h+1$. Avec $\xi_t=0$ on trouve donc que $S_{GT}(\boldsymbol\theta)=\sigma^2S_g(\boldsymbol\theta)$.

A.2.2 Équivalence avec les moindres carrés pondérés

Du fait de la forme des filtres obtenus par la méthode de Grun-Rehomme, Guggemos, et Ladiray (2018), lorsque les contraintes imposées sont la préservation des tendances de degré $d$, celle-ci est équivalente à une estimation locale d’une tendance polynomiale de degré $d$ par moindres carrés généralisés. En effet, dans ce cas, la solution est $\hat{\boldsymbol \theta} = \boldsymbol \Sigma^{-1}\boldsymbol X_p'\left(\boldsymbol X_p\boldsymbol \Sigma^{-1}\boldsymbol X_p'\right)^{-1}\boldsymbol e_1$ avec $\boldsymbol \Sigma=\alpha \boldsymbol F+\beta \boldsymbol S+ \gamma \boldsymbol T$, et c’est l’estimation de la constante obtenue par moindres carrés généralisés lorsque la variance des résidus est $\boldsymbol \Sigma$. L’équivalence entre les deux méthodes peut donc se voir comme un cas particulier de l’équivalence entre les moindres carrés pondérés et les moindres carrés généralisés. C’est par exemple le cas des filtres symétriques d’Henderson qui peuvent s’obtenir par les deux méthodes.

Dans ce sens, Henderson (1916) a montré que les poids $\boldsymbol w=(w_{-p},\dots, w_{f})$ associés à une moyenne mobile issue de la régression polynomiale locale par moindres carrés pondérés pouvaient s’écrire sous la forme : \[ w_i = \kappa_i P\left(\frac{i}{p+f+1}\right)\text{ où }P\text{ est un polynôme de degré }d. \] Il a également montré l’inverse : toute moyenne mobile $\boldsymbol \theta=(\theta_{-p},\dots, \theta_{f})$ qui préserve les tendances de degré $d$ et dont le diagramme des coefficients (c’est-à-dire la courbe de $\theta_t$ en fonction de $t$) change au plus $d$ fois de signes peut être obtenue par une régression polynomiale locale de degré $p$ estimée par moindres carrés pondérés. Pour cela il suffit de trouver un polynôme $P\left(\frac{X}{p+f+1}\right)$ de degré inférieur ou égal à $d$ et dont les changements de signes coïncident avec les changements de signes de $\boldsymbol \theta$. Le noyau associé est alors $\kappa_i=\frac{ \theta_i}{P\left(\frac{i}{p+f+1}\right)}$. C’est le cas de tous les filtres symétriques issus de l’approche FST et de la majorité des filtres asymétriques (figure 15).

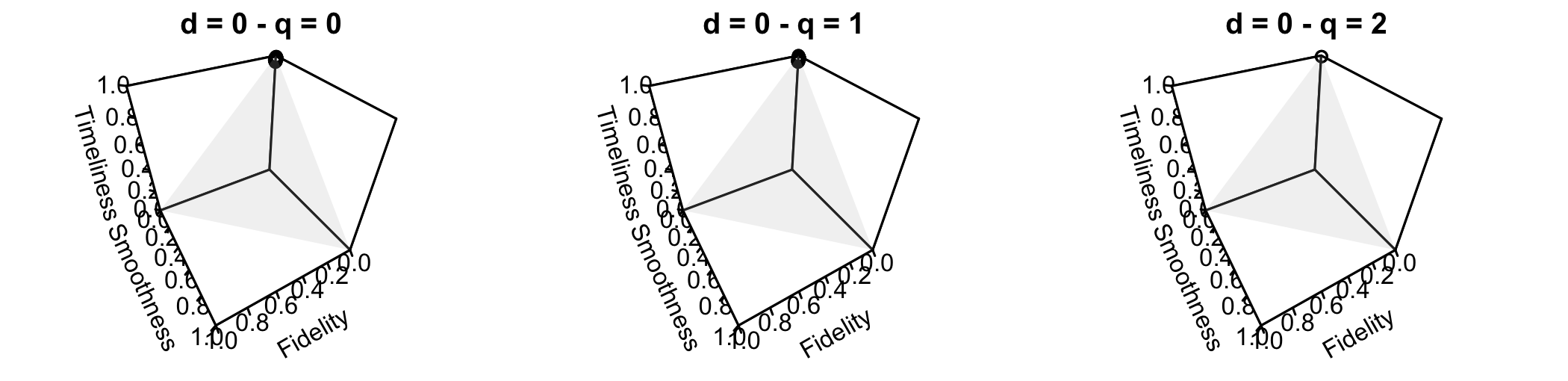
Ensemble des poids pour lesquels la méthode FST n'est pas équivalente aux moindres carrés pondérés pour $h=6$ (filtre symétrique de 13 termes), sous contrainte de préservation des polynômes de degré au plus 3 ($d=0,1,2,3$).

Figure 15 : Ensemble des poids pour lesquels la méthode FST n’est pas équivalente aux moindres carrés pondérés pour $h=6$ (filtre symétrique de 13 termes), sous contrainte de préservation des polynômes de degré au plus 3 ($d=0,1,2,3$).

La smoothness est calculée avec le paramètre $d=3$ ($S_g(\boldsymbol \theta) = \sum_{j}(\nabla^{3}\theta_{j})^{2}$), comme pour le filtre symétrique d’Henderson.

Les poids sont calculés à partir d’un quadrillage de 200 points de l’intervalle $[0,1]$ et en ne gardant que ceux tels que leur somme fasse 1.

Lorsque tous les filtres FST sont équivalents à une approche polynomiale, aucun graphique n’est tracé. Pour un filtre symétrique de 13 ermes, la méthode FST est donc équivalente à une approche polynômiale sauf lorsqu’on ne contraint que la préservation des constante ($d=0$), pour les filtres nécessitant au plus deux observations futures ($q=0,1$ ou 2) et seulement lorsque le poids associé à la timeliness est proche de 1.

Plus récemment, Luati et Proietti (2011) se sont intéressés aux cas d’équivalences entre les moindres carrés pondérés et les moindres carrés généralisés pour déterminer des noyaux optimaux (au sens de Gauss-Markov). Ils montrent que le noyau d’Epanechnikov est le noyau optimal associé à la régression polynomiale locale où le résidu, $\varepsilon_t$, est un processus moyenne mobile (MA) non inversible d’ordre 1 (i.e., $\varepsilon_t=(1-B)\xi_t$, avec $\xi_t$ un bruit blanc). Dans ce cas, la matrice $\boldsymbol \Sigma$ de variance-covariance correspond à la matrice obtenue par le critère de smoothness avec le paramètre $q=2$ ($\sum_{j}(\nabla^{2}\theta_{j})^{2} = \boldsymbol \theta'\boldsymbol \Sigma\boldsymbol \theta$) : il y a donc équivalence avec l’approche FST. De même, le noyau d’Henderson est le noyau optimal associé à la régression polynomiale locale où le résidu est un processus moyenne mobile (MA) non inversible d’ordre 2 (i.e., $\varepsilon_t=(1-B)^2\xi_t$, avec $\xi_t$ un bruit blanc).

A.2.3 RKHS et polynômes locaux

Comme montré dans la section précédente, la théorie des espaces de Hilbert à noyau reproduisant permet de reproduire les filtres symétriques par approximation polynomiale locale. Comme le montrent Luati et Proietti (2011), cette théorie permet donc également de reproduire les filtres directs asymétriques (DAF), qui sont équivalents à l’approximation polynomiale locale mais en utilisant une fenêtre d’estimation asymétrique. Cependant, ils ne peuvent pas être obtenus par la formalisation de Dagum et Bianconcini (2008) mais par une discrétisation différente de la formule (11) : \[ K_{d+1}(t)=\frac{\det{\boldsymbol H_{d+1}[1,\boldsymbol x_t]}}{\det{\boldsymbol H_{d+1}}}f_0(t), \] où $\boldsymbol H_{d+1}[1,\boldsymbol x_t]$ est la matrice obtenue en remplaçant la première ligne de $\boldsymbol H_{d+1}$ par $\boldsymbol x_t=\begin{pmatrix} 1 & t & t^2 & \dots & t^d\end{pmatrix}'$. Dans le cas discret, $f_0(t)$ est remplacé par $\kappa_j$ et en remplaçant les moments théoriques par les moments empiriques $\boldsymbol H_{d+1}$ devient $\boldsymbol X'_p\boldsymbol K_p\boldsymbol X_p$ et les coefficients du filtre asymétrique sont obtenus en utilisant la formule : \[ w_{a,j}=\frac{\det{\boldsymbol X'_p\boldsymbol K_p\boldsymbol X_p[1,\boldsymbol x_j]} }{ \det{\boldsymbol X'_p\boldsymbol K_p\boldsymbol X_p} }\kappa_j. \] En effet, la règle de Cramer permet de trouver une solution explicite à l’équation des moindres carrés $(\boldsymbol X'_p\boldsymbol K_p\boldsymbol X_p)\hat{\boldsymbol \beta}=\boldsymbol X'_p\boldsymbol K_p \boldsymbol y_p$ où $\hat \beta_0=\hat m_t$ : \[ \hat \beta_0 = \frac{\det{\boldsymbol X'_p\boldsymbol K_p\boldsymbol X_p[1,\boldsymbol b]}}{\det{\boldsymbol X'_p\boldsymbol K_p\boldsymbol X_p}}f_0(t) \quad\text{où}\quad \boldsymbol b=\boldsymbol X'_p\boldsymbol K_p\boldsymbol y_p. \] Comme $\boldsymbol b=\sum_{j=-h}^q\boldsymbol x_j\kappa_jy_{t+j}$ il vient : \[ \det{\boldsymbol X'_p\boldsymbol K_p\boldsymbol X_p[1,\boldsymbol b]} = \sum_{j=-h}^q\det{\boldsymbol X'_p\boldsymbol K_p\boldsymbol X_p[1,\boldsymbol x_j]}\kappa_jy_{t+j}. \] Et enfin : \[ \hat \beta_0 = \hat m_t= \sum_{j=-h}^q\frac{\det{\boldsymbol X'_p\boldsymbol K_p\boldsymbol X_p[1,\boldsymbol x_j]} }{ \det{\boldsymbol X'_p\boldsymbol K_p\boldsymbol X_p} }\kappa_j y_{t+j}. \]

A.3 Diagrammes synthétiques

Les figures 16 et 17 résument les liens entre toutes les méthodes.

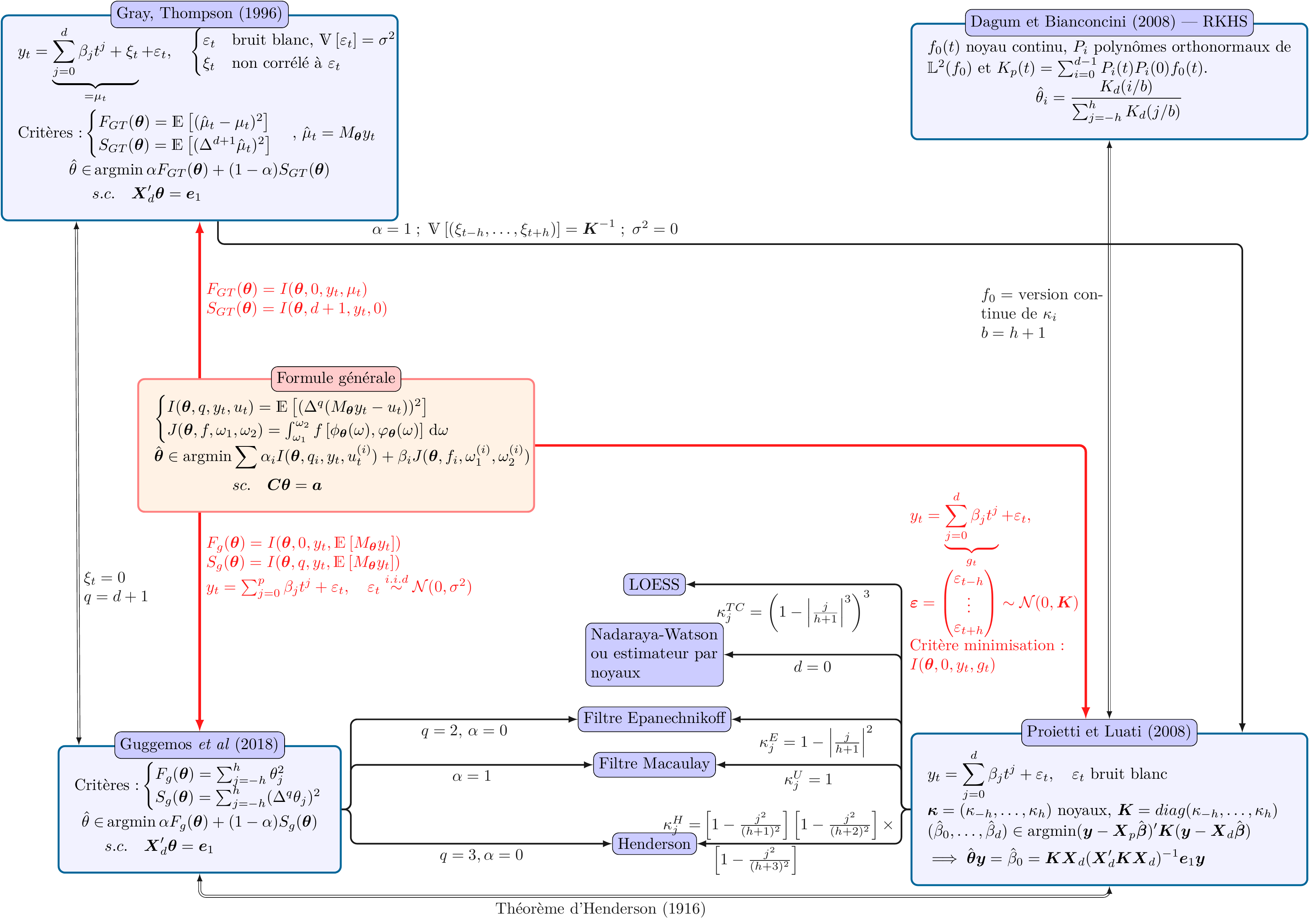
$Synthèse des méthodes de construction de moyennes mobiles symétriques $\boldsymbol\theta=(\theta_{-h},\dots,\theta_{h})$ de $2h+1$ termes.$

Figure 16 : Synthèse des méthodes de construction de moyennes mobiles symétriques $\boldsymbol\theta=(\theta_{-h},\dots,\theta_{h})$ de $2h+1$ termes.

$\boldsymbol X = \boldsymbol X_d = \begin{pmatrix} \boldsymbol x_0 \quad\cdots \quad \boldsymbol x_d \end{pmatrix}$ avec $\boldsymbol x_i=\begin{pmatrix} (-h)^i \quad \cdots \quad (h)^i\end{pmatrix}'$.

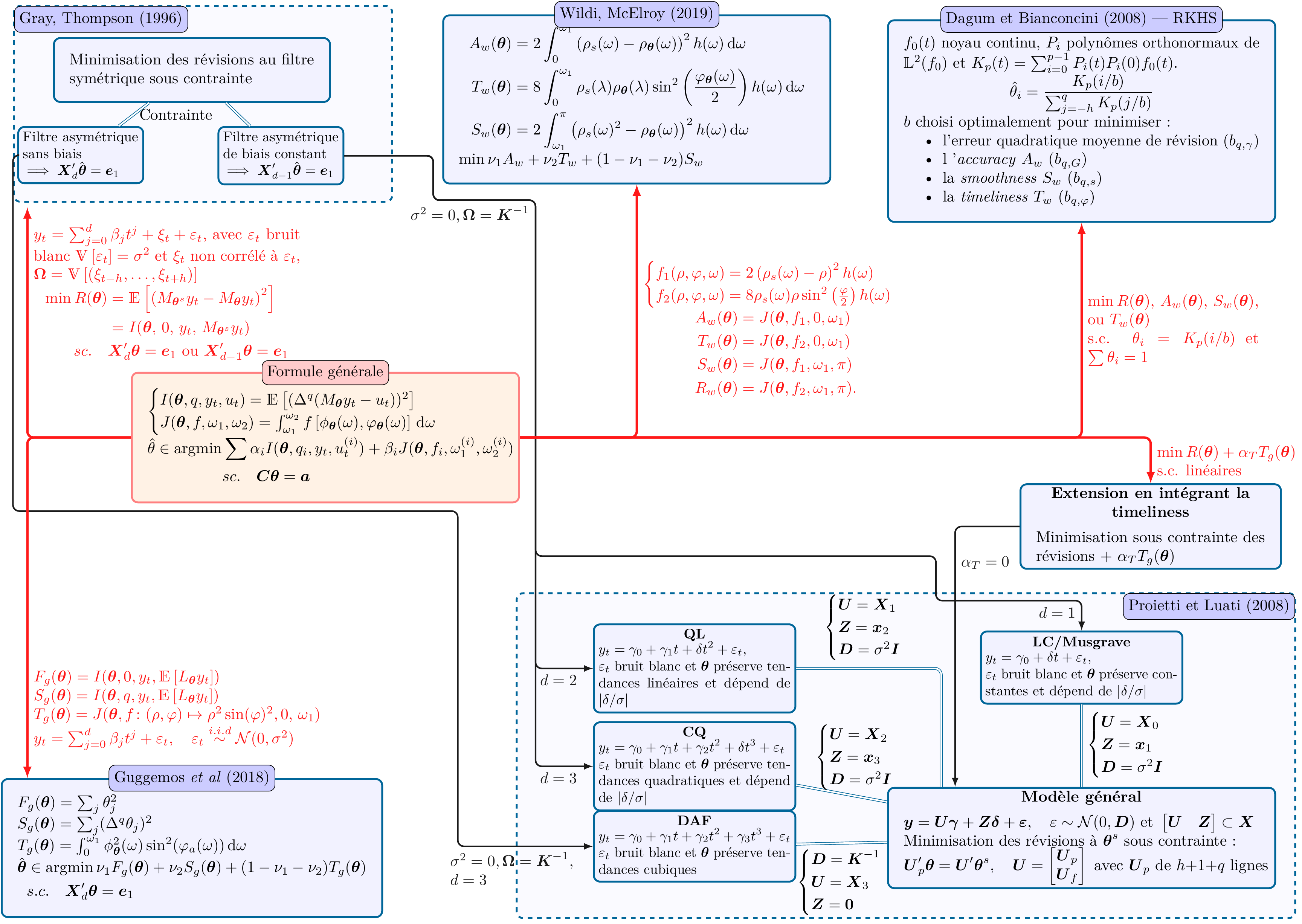
$Synthèse des méthodes de construction de moyennes mobiles asymétriques $\boldsymbol\theta=(\theta_{-h},\dots,\theta_{q})$, $0\leq q< h$ avec $\boldsymbol\theta^s$ le filtre symétrique de référence de $2h+1$ termes.$

Figure 17 : Synthèse des méthodes de construction de moyennes mobiles asymétriques $\boldsymbol\theta=(\theta_{-h},\dots,\theta_{q})$, $0\leq q< h$ avec $\boldsymbol\theta^s$ le filtre symétrique de référence de $2h+1$ termes.

$\boldsymbol X_d = \begin{pmatrix} \boldsymbol x_0 \quad\cdots \quad \boldsymbol x_d \end{pmatrix}$ avec $\boldsymbol x_i=\begin{pmatrix} (-h)^i \quad \cdots \quad (q)^i\end{pmatrix}'$ et $\boldsymbol X=\boldsymbol X_d$ avec $q=h$.

Références

Dagum, Estela Bee, et Silvia Bianconcini. 2008. « The Henderson Smoother in Reproducing Kernel Hilbert Space ». Journal of Business & Economic Statistics 26: 536‑45. https://ideas.repec.org/a/bes/jnlbes/v26y2008p536-545.html.

Gray, Alistair, et Peter Thomson. 1996. « Design of Moving-Average Trend Filters using Fidelity and Smoothness Criteria ». In Athens Conference on Applied Probability and Time Series Analysis, édité par P. M. Robinson et Murray Rosenblatt, 205‑19. New York, NY: Springer New York. https://www.census.gov/library/working-papers/1996/adrm/rr96-01.html.

Grun-Rehomme, Michel, Fabien Guggemos, et Dominique Ladiray. 2018. « Asymmetric Moving Averages Minimizing Phase Shift ». Handbook on Seasonal Adjustment. ec.europa.eu/eurostat/web/products-manuals-and-guidelines/-/KS-GQ-18-001.

Henderson, Robert. 1916. « Note on graduation by adjusted average ». Transactions of the actuarial society of America 17: 43‑48.

Luati, Alessandra, et Tommaso Proietti. 2011. « On the equivalence of the weighted least squares and the generalised least squares estimators, with applications to kernel smoothing ». Annals of the Institute of Statistical Mathematics 63 (4): 851‑71. https://doi.org/10.1007/s10463-009-0267-8.

Proietti, Tommaso, et Alessandra Luati. 2008. « Real time estimation in local polynomial regression, with application to trend-cycle analysis ». Ann. Appl. Stat. 2 (4): 1523‑53. https://doi.org/10.1214/08-AOAS195.

———. 2019. « The trilemma between accuracy, timeliness and smoothness in real-time signal extraction ». International Journal of Forecasting 35 (3): 1072‑84. https://EconPapers.repec.org/RePEc:eee:intfor:v:35:y:2019:i:3:p:1072-1084.

La série de référence est en général un estimateur robuste de la tendance-cycle de $Y_t$ que l’on cherche à approcher par application de la moyenne mobile $M_{\boldsymbol\theta}$ sur les observations $y_t$. Cet estimateur peut également dépendre de $M_{\boldsymbol\theta}.$↩︎