Calcul numérique avec NumPy

En tant que statisticien, on est fréquemment amené à manipuler des séries de valeurs numériques, à partir desquelles on réalise diverses opérations mathématiques, des plus usuelles (moyenne, variance, etc.) aux plus complexes. On peut, comme on l’a fait dans les précédents tutoriels, utiliser les objets fondamentaux de Python, et en particulier les listes, pour réaliser de telles opérations. En pratique, on préférera utiliser la librairie de référence pour le calcul scientifique, NumPy, qui fournit à la fois des objets (les arrays) et des fonctions qui vont grandement nous simplifier la vie pour effectuer tous nos calculs en Python de manière efficiente.

NumPy

On commence par importer la librairie NumPy. Comme expliqué dans un précédent tutoriel, l’usage est courant est de lui attribuer l’alias np.

import numpy as np

Pourquoi utiliser NumPy ?

Plutôt que de présenter de manière abstraite les avantages de NumPy, illustrons ces derniers à travers un exemple simple : la multiplication terme à terme de deux vecteurs.

On génère deux vecteurs contenant les entiers allant de \(0\) à \(99999\), que l’on multiplie terme à terme. On effectue cela d’abord via les listes Python (fonction mult_list), puis à l’aide de NumPy (fonction mult_np), et on compare les performances des deux méthodes.

def mult_list(n):
    a = range(n)
    b = range(n)

    c = []
    for i in range(len(a)):
        mult = a[i] * b[i]
        c.append(mult)
        
    return c

def mult_np(n):
    a_np = np.arange(n)
    b_np = np.arange(n)
    
    c_np = a_np * b_np

    return c_np

n = 100000

# Vérification de la cohérence sur les 10 premiers éléments
print(mult_list(n)[:10])
print(mult_np(n)[:10])

[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
[ 0  1  4  9 16 25 36 49 64 81]

%%timeit -n10

mult_list(n)  # Performance de la méthode liste

16.4 ms ± 147 μs per loop (mean ± std. dev. of 7 runs, 10 loops each)

%%timeit -n10

mult_np(n)  # Performance de la méthode NumPy

126 μs ± 34.3 μs per loop (mean ± std. dev. of 7 runs, 10 loops each)

Cet exemple illustre à lui seul les principaux avantages de NumPy pour le calcul scientifique :

• les calculs sont vectorisés : multiplier deux arrays va naturellement effectuer la multiplication terme à terme, contrairement aux listes qui ne permettent pas cette opération. Les personnes travaillant avec R retrouveront là une propriété familière et bien pratique.

• conséquence de la vectorisation, la syntaxe est plus légère et plus claire : on voit directement l’opération qui est effectuée et on limite ainsi les risques d’erreur ;

• les calculs sont automatiquement optimisés par NumPy (via l’appel à du code C pré-compilé), réduisant très largement le temps mis par les opérations mathématiques (divisé par un facteur 10 dans notre exemple).

Les array NumPy

Définition

Toute la librairie NumPy est basée sur un objet fondamental : l’array. Un array est un objet qui contient une séquence de données, et présente deux caractéristiques principales :

• les données contenues dans un array doivent être de type homogène, là où une même liste peut contenir des objets de différente nature ;

• un array a une taille fixée à sa création, là où une liste peut grandir dynamiquement (en ajoutant des éléments via la méthode append par exemple).

Ce sont en grande partie ces deux contraintes qui rendent possible les gains de performance et la syntaxe lisible qu’offre NumPy.

Création

Il existe différentes manières de créer un array. La plus standard est de convertir une liste en array via la fonction array de NumPy.

l = [1, 2, 3]
a = np.array(l)
print(a)

[1 2 3]

A première vue, la fonction print renvoie une représentation identique à celle d’une liste. Vérifions le type de notre objet.

type(a)

numpy.ndarray

L’objet est de type ndarray, qui est le type standard correspondant à un array NumPy.

On a vu qu’un array avait pour propriété de contenir des données de type homogène ; en l’occurrence, des entiers. On peut vérifier le type des données contenues via l’attribut dtype d’un array.

a.dtype

dtype('int64')

Même si NumPy est avant tout une librairie dédiée au calcul numérique, il reste tout à fait possible de définir des arrays contenant des chaînes de caractères.

b = np.array(['1', 'tigre'])
b.dtype

dtype('<U5')

Le dtype par défaut des arrays contenant des chaînes de caractères est un peu particulier, mais cela n’a pas d’importance en pratique. Retenez simplement sa forme.

Enfin, question importante : que se passe-t-il si l’on essaie de définir un array contenant des objets de types hétérogènes ?

c = np.array([1, 2, '3'])
print(c)
print(c.dtype)

['1' '2' '3']
<U21

Réponse : tous les objets sont convertis en chaîne de caractères par défaut.

Dimension

Les array correspondent en fait à des tableaux de données, c’est à dire qu’ils peuvent être uni- ou multi-dimensionnels. Un array de dimension 1 ressemble à un vecteur (ou une liste), un array de dimension 2 ressemble à une matrice, et ainsi de suite.

On peut afficher le nombre de dimensions d’un array via l’attribut ndim.

c = np.array([1, 2, '3'])
c.ndim

1

De la même manière que l’on a créé un array de dimension 1 à partir d’une liste simple, on peut créer un array multi-dimensionnel à partir d’une liste de listes.

d = np.array([[1, 2, 3], [4, 5, 6]])
print(d)

[[1 2 3]
 [4 5 6]]

On a converti une liste contenant 2 sous-listes à 3 éléments chacune, ce qui donne un array à deux dimensions. Notons que l’appel de print affiche une matrice à deux lignes et trois colonnes.

d.ndim

2

On a bien affaire à un array à deux dimensions. Mais en pratique, lorsqu’on manipule des arrays multidimensionnels, on a aussi envie de connaître la taille de chacune des dimensions. En dimension 2, c’est le nombre de lignes et de colonnes. Pour cela, on utilise la méthode shape, qui renvoie un tuple contenant les tailles des différentes dimensions.

d.shape

(2, 3)

Le premier chiffre donne le nombre de lignes, le second le nombre de colonnes. On reviendra par la suite sur l’ordre des dimensions à travers la notion d’axis.

Indexation

On accède aux différents éléments d’un array de dimension 1 exactement de la même manière que ceux d’une liste.

a = np.array([1, 2, 3, 4, 5, 6])

print(a)
print()
print(a[1])
print()
print(a[2:5])
print()
print(a[-2])

[1 2 3 4 5 6]

2

[3 4 5]

5

Pour un array multidimensionnel, il faut spécifier le ou les éléments voulus sur chacune des dimensions de l’array, en les séparant par des virgules.

b = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

print(b)
print()
print(b[1, 3])
print()
print(b[1:3, 1:3])

[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]

8

[[ 6  7]
 [10 11]]

Pour accéder à une ligne complète, on peut utiliser : sur la dimension des colonnes pour spécifier : “toutes les colonnes”. Et inversement pour récupérer une colonne complète.

print(b[1,:])
print()
print(b[:,2])

[5 6 7 8]

[ 3  7 11]

Modification d’éléments

Les éléments d’un array peuvent être modifiés. On combine pour cela la syntaxe d’indexation vue précédemment avec l’opérateur d’assignation =.

b = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

b[1, 1] = 18
print(b)

[[ 1  2  3  4]
 [ 5 18  7  8]
 [ 9 10 11 12]]

On peut également modifier des séries de nombres, voire des lignes/colonnes complètes, à condition d’assigner un élément de même taille.

b = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

b[:, 2] = [-1, -1, -1]
b

array([[ 1,  2, -1,  4],
       [ 5,  6, -1,  8],
       [ 9, 10, -1, 12]])

Contrairement aux listes, on ne va généralement pas ajouter ou supprimer d’éléments à un array. La raison est que, comme indiqué précédemment, la taille d’un array est fixée à sa construction.

Si l’on souhaite faire grandir un array, on va généralement le faire à partir d’une liste – qui elle peut grandir – que l’on convertit ensuite en array.

Si l’on souhaite supprimer des éléments d’un array, on peut utiliser la syntaxe d’indexation étudiée dans la section précédente pour récupérer le sous-array qui nous intéresse, et assigner ce dernier à une nouvelle variable.

Masques booléens

Un gros avantage des arrays NumPy par rapport aux listes est qu’ils supportent les masques booléens, c’est à dire qu’on peut sélectionner des éléments d’un array en lui passant un array de même taille contenant des booléens.

a = np.array([1, 2, 3])
a[[True, True, False]]

array([1, 2])

Cette propriété ouvre de nombreuses possibilités, dans la mesure où elle peut être combinée avec la propriété de vectorisation des arrays. Il devient ainsi très facile de sélectionner des éléments selon des conditions, même pour les arrays multidimensionnels.

b = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
cond = (b > 6) & (b != 10)

print(cond)
print()
print(b[cond])

[[False False False False]
 [False False  True  True]
 [ True False  True  True]]

[ 7  8  9 11 12]

Et l’on peut bien entendu exploiter ce mécanisme pour modifier des éléments selon une condition.

b[cond] = -1
print(b)

[[ 1  2  3  4]
 [ 5  6 -1 -1]
 [-1 10 -1 -1]]

Ce dernier exemple illustre par ailleurs une propriété importante en NumPy appelée broadcasting : lorsque l’on remplace plusieurs éléments d’un array par un élément de taille 1 (et non un array de même taille), tous les éléments sont remplacés par cette valeur.

Opérations mathématiques

Arithmétique sur les arrays

Tout au début de ce tutoriel, nous avons vu que multiplier deux arrays via l’opérateur * effectuait une multiplication termes à termes des deux arrays, et ce de manière vectorisée. Les opérations élémentaires (+, -, * et /) s’appliquent de la même manière aux arrays multidimensionnels.

a = np.array([[1, 2, 2], [2, 2, 1]])
b = np.array([[3, 3, 1], [1, 3, 3]])

a * b

array([[3, 6, 2],
       [2, 6, 3]])

Notons qu’on retrouve la propriété de broadcasting discutée dans la section précédente : lorsque l’on effectue une opération entre un array et un nombre de taille 1, l’opération est appliquée à chaque terme de l’array.

a * 4

array([[4, 8, 8],
       [8, 8, 4]])

Algèbre linéaire

NumPy permet de réaliser simplement et de manière efficiente des opérations d’algèbre linéaire sur les arrays. L’ensemble des fonctions disponibles sont présentées dans la documentation officielle (en Anglais).

Par exemple, l’opérateur @ permet de réaliser une multiplication matricielle (et non plus termes à termes comme le fait *).

a = np.array([[1, 2, 3], [3, 2, 1]])
b = np.array([[2, 3], [1, 3], [3, 1]])

a @ b

array([[13, 12],
       [11, 16]])

Fonctions mathématiques

NumPy offre pléthore de fonctions mathématiques et statistiques, comme sum, mean, min, round, log, etc. Leur application à des objets unidimensionnels ne pose pas de problème particulier.

print(np.log(12))
print()
print(np.min([1, 2, 3]))
print()
print(np.mean([1, 2, 3]))

2.4849066497880004

1

2.0

En revanche, dans le cas multidimensionnel, leur utilisation devient un peu plus subtile car on peut vouloir réaliser l’agrégation selon différentes dimensions. Si l’on ne spécifie rien, l’agrégation est effectuée sur tous les éléments de l’array.

a = np.array([[1, 2, 2], [2, 2, 1]])

np.sum(a)

np.int64(10)

Mais comment faire si l’on veut sommer par ligne ? Ou bien par colonne ? C’est là qu’intervient un élément crucial et assez complexe des fonctions de NumPy : le paramètre axis, qui spécifie la dimension selon laquelle est effectuée l’opération.

Lorsqu’il n’est pas spécifié comme dans l’exemple précédent, il prend la valeur None par défaut.

a = np.array([[1, 2, 2], [2, 2, 1]])

np.sum(a, axis=None)  # idem que np.sum(a)

np.int64(10)

La figure suivante permet de bien se représenter la manière dont fonctionnent les axes avec NumPy, afin de bien spécifier le sens attendu de l’agrégation.

axis

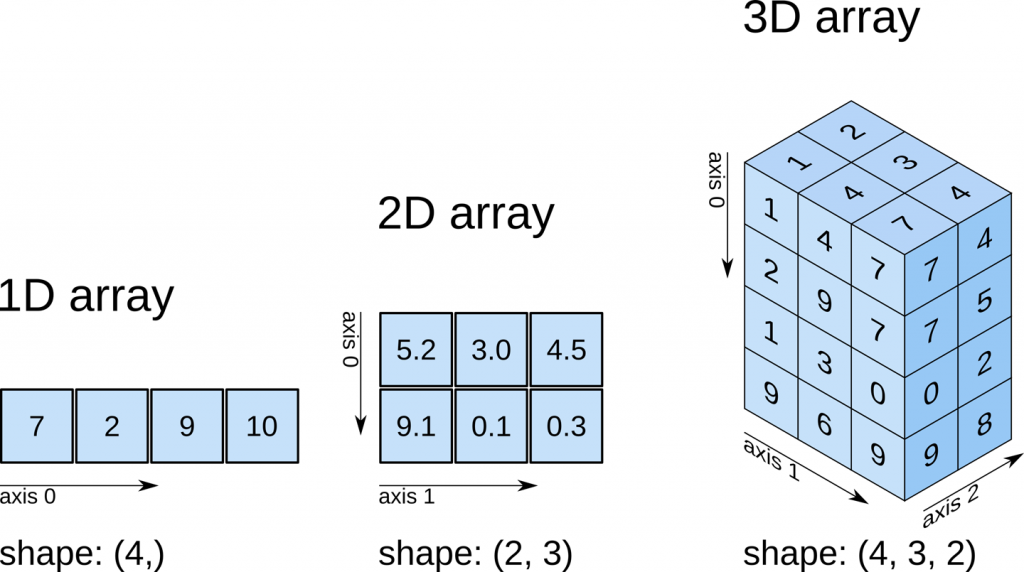
Ainsi, si l’on souhaite calculer la somme de chaque colonne par exemple, il faut agréger selon l’axe \(0\).

a = np.array([[1, 2, 2], [2, 2, 1]])

np.sum(a, axis=0)

array([3, 4, 3])

Et inversement pour obtenir les sommes de chaque ligne.

np.sum(a, axis=1)

array([5, 5])

Enfin, notons que les fonctions mathématiques qui réalisent une agrégation sont généralement également disponibles comme méthodes d’un array. Elles fonctionnent de la même manière, au détail près qu’elles ne prennent pas l’array en argument dans la mesure où elles sont déjà “attachées” à celui-ci.

a.sum(axis=1)

array([5, 5])

Conclusion

NumPy est la librairie quasi-standard de calcul scientifique en Python. Elle est à privilégier dès lors que vous souhaitez effectuer des opérations sur des données numériques, a fortiori lorsqu’il s’agit d’opérations vectorisées et/ou mobilisant des objets multidimensionnels comme des matrices.

Les possibilités offertes par NumPy sont gigantesques, et nous n’en avons vu qu’un aperçu. La documentation officielle présente l’ensemble de ces possibilités. Cette cheat sheet peut également s’avérer utile en cas d’oubli. Nous verrons également des fonctions supplémentaires à travers les exercices de fin de chapitre.

Exercices

Questions de compréhension

• 1/ Quels sont les principaux avantages de NumPy ?

• 2/ Quelles sont les deux caractéristiques principales d’un array NumPy ?

• 3/ Que se passe-t-il si l’on essaie de définir un array contenant des objets de types hétérogènes ?

• 4/ Quelle est la principale méthode pour créer un array ?

• 5/ Quelles informations contient l’attribut shape d’un array ?

• 6/ Peut-on ajouter un élément à un array ? Supprimer un élément ?

• 7/ Qu’est-ce qu’un masque booléen et à quoi cela sert-il ?

• 8/ Qu’est-ce que la propriété de broadcasting ?

• 9/ A quoi sert le paramètre axis des fonctions mathématiques de NumPy ?

Afficher la solution

• 1/ Les calculs sont vectorisés, ce qui simplifie grandement la syntaxe et réduit donc les risques d’erreur. Par ailleurs, les calculs sont optimisés automatiquement par NumPy, ce qui accroît très fortement les performances.

• 2/ Les données contenues dans un array doivent être de type homogène. Un array a une taille fixée lors de sa création.

• 3/ Tous les objets sont interprétés comme des chaînes de caractères.

• 4/ Créer une liste et la convertir ensuite en array via la fonction np.array.

• 5/ L’attribut shape d’un array renvoie un tuple qui contient la taille de chaque dimension, et donc également le nombre de dimensions.

• 6/ Il existe des fonctions qui effectuent ces opérations, mais elles ne sont pas très utilisées en pratique, dans la mesure où un array est de taille fixée lors de sa création.

• 7/ Un masque booléen est un array de valeurs booléennes (True et False), que l’on va utiliser pour sélectionner des éléments d’un autre array. C’est notamment très pratique pour sélectionner des éléments selon une condition (test).

• 8/ Lorsqu’on effectue une opération entre un array et une valeur de taille 1 (typiquement, un entier ou un réel), l’opération est appliquée à chaque élément de l’array.

• 9/ Le paramètre axis sert à spécifier la dimension selon laquelle on souhaite performer une agrégation (fonction math, stat..).

Manipulations simples des données d’un DataFrame

Un vecteur comprenant les entiers compris entre 10 et 20 est défini dans la cellule suivante. En utilisant l’indexation des arrays NumPy :

• sélectionner les éléments aux positions 1, 3 et 4

• sélectionner tous les éléments sauf le premier

• sélectionner tous les éléments sauf le premier et le dernier

• sélectionner les 3 premiers éléments

• sélectionner les 5 derniers éléments

• sélectionner tous les éléments pairs

• sélectionner tous les éléments en les triant dans l’ordre inverse (NB : la fonction np.flip permet de faire la même chose)

X = np.arange(10, 21)

print(X)

[10 11 12 13 14 15 16 17 18 19 20]

# Testez votre réponse dans cette cellule

Afficher la solution

X = np.arange(10, 21)

print(X[[1, 3, 4]])
print(X[1:])
print(X[1:-1])
print(X[:3])
print(X[-5:])
print(X[::2])
print(X[::-1])

Sélectionner des éléments dans une matrice

Une matrice de taille 5x5 comprenant tous les entiers compris entre 0 et 24 est définie dans la cellule suivante. En utilisant l’indexation des arrays NumPy :

• sélectionner la valeur \(19\)

• sélectionner la 2ème ligne

• sélectionner la 4ème colonne

• sélectionner la sous-matrice 3x3 centrale

• sélectionner les éléments diagonaux (NB : la fonction np.diag permet de réaliser la même opération de manière beaucoup plus simple)

Y = np.arange(0, 25).reshape((5, 5))

print(Y)

[[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]
 [15 16 17 18 19]
 [20 21 22 23 24]]

# Testez votre réponse dans cette cellule

Afficher la solution

Y = np.arange(0, 25).reshape((5, 5))

print(Y[3, 4])
print(Y[1, :])
print(Y[:, 3])
print(Y[1:4, 1:4])
print(Y[np.arange(0, 5), np.arange(0, 5)])

Un peu de calcul

Deux matrices carrées de taille 3x3 sont définies sous forme d’arrays NumPy dans la cellule suivante. A partir de ces matrices, réaliser les opérations mathématiques suivantes :

• multiplier tous les éléments de X par 3

• diviser les éléments de Y par ceux de X

• passer tous les éléments de Y au log

• passer tous les éléments de X au carré

• faire une multiplication matricielle de X et Y

• transposer la matrice Y

NB : vous pourrez trouver les fonctions nécessaires dans la documentation ou via un moteur de recherche.

X = np.array([[1,2,3],
              [4,5,6],
              [7,8,9]])

Y = np.array([[10,11,12],
              [13,14,15],
              [16,17,18]])

# Testez votre réponse dans cette cellule

Afficher la solution

X = np.array([[1,2,3],
              [4,5,6],
              [7,8,9]])

Y = np.array([[10,11,12],
              [13,14,15],
              [16,17,18]])

print(3 * X)
print()
print(Y / X)
print()
print(np.log(Y))
print()
print(np.square(X))
print()
print(Y @ X)
print()
print(Y.T)

Initialisation d’arrays de diverses natures

Dans le tutoriel, nous avons vu que la méthode standard pour créer un array NumPy consistait à initialiser une liste, que l’on convertit ensuite en array. On peut également utiliser des fonctions natives de NumPy qui créent des array d’une taille donnée, contenant des valeurs basiques (ex : valeurs “quasi-vides”, zéros, uns, une valeur spécifiée par l’utilisateur, etc.).

Par exemple, pour créer une matrice à 3 lignes et deux colonnes contenant des zéros, la syntaxe est :

np.zeros((3, 2))

array([[0., 0.],
       [0., 0.],
       [0., 0.]])

En vous référant à la documentation de ces fonctions, générer :

• un vecteur (array à 1 dimension), contenant 18 fois la valeur \(1\) (fonction np.ones)

• un array à 3 dimensions, respectivement de tailles 2, 3 et 5, contenant uniquement des zéros (fonction np.zeros)

• une matrice (array à 2 dimensions), à 4 lignes et 3 colonnes, contenant uniquement la valeur 5 (fonction np.full)

• une matrice identité de taille 5, i.e. une matrice à 5 lignes et 5 colonnes, contenant des \(1\) sur sa diagonale et des \(0\) partout ailleurs (fonction np.eye)

• un vecteur contenant les entiers compris entre \(0\) à \(99\) inclus (fonction np.arange)

• un vecteur contenant les entiers pairs compris entre \(0\) à \(99\) inclus (fonction np.arange)

• un vecteur contenant 5 valeurs uniformément espacées entre \(2\) et \(3\) inclus (fonction np.linspace)

# Testez votre réponse dans cette cellule

Afficher la solution

a = np.ones((18,))
print(a)
print()

b = np.zeros((2, 3, 5))
print(b)
print()

c = np.full((4, 3), fill_value=5)
print(c)
print()

d = np.eye(5)
print(d)
print()

e = np.arange(0, 100)
print(e)
print()

x = np.arange(0, 100, step=2)
print(x)
print()

y = np.linspace(2.0, 3.0, num=5)
print(y)
print()

Tirage d’un vecteur selon une loi normale

En vous référant à la documentation des fonctions de génération de nombres aléatoires de NumPy, générer un vecteur X de taille 10000, contenant des nombres tirés selon une loi normale de moyenne 0 et de variance 2.

Vérifiez ensuite à l’aide des fonctions mathématiques de NumPy que la moyenne et la variance de votre échantillon sont cohérents par rapport aux valeurs attendues.

Indice : attention à la manière dont est spécifiée la variance dans la fonction NumPy de génération d’une loi normale.

# Testez votre réponse dans cette cellule

Afficher la solution

X = np.random.normal(0, np.sqrt(2), 10000)

print(np.mean(X), np.var(X))

Tirage d’une matrice selon une loi uniforme

En vous référant à la documentation des fonctions de génération de nombres aléatoires de NumPy, générer une matrice U de taille 1000 par 1000, contenant des nombres tirés selon une loi uniforme dans l’intervalle [-1, 1].

En utilisant la fonction np.all et un test booléen, vérifier que tous les nombres contenus dans U sont bien compris entre -1 et 1.

# Testez votre réponse dans cette cellule

Afficher la solution

N = 1000
U = np.random.uniform(-1, 1, size=(N, N))

np.all((U >= -1) & (U <= 1))

Binariser une matrice de nombres

On peut parfois avoir besoin de binariser une matrice numérique, c’est à dire de fixer un seuil au delà duquel les valeurs numériques sont fixées à 1, et à 0 en-dessous. NumPy propose plusieurs méthodes pour réaliser une telle opération, nous allons en voir deux.

Dans la cellule suivante, une matrice X à 6 lignes et 6 colonnes est générée, qui comprend des entiers aléatoirement choisis entre 0 et 49. Vous devez binariser cette matrice de deux manières différentes sans l’écraser (i.e. la matrice binaire doit être assignée à une autre variable que X et X ne doit pas être modifiée) :

• première méthode : en utilisant la fonction np.zeros et les masques booléens

• seconde méthode : en utilisant la fonction np.where (cf. doc)

X = np.random.randint(0, 50, size=(6, 6))

# Testez votre réponse dans cette cellule

Afficher la solution

X = np.random.randint(0, 50, size=(6, 6))

# Première possibilité : via les masques booléens
A = np.zeros((6, 6))
A[X > 25] = 1

# Deuxième possibilité : via la fonction np.where
B = np.where(X > 25, 1, 0)

print(X)
print()
print(A)
print()
print(B)

Touché-coulé

L’objectif de cet exercice est de programmer seulement à l’aide d’objets et de fonctions de NumPy un touché-coulé très basique.

Une grille de 5x5 est définie dans la cellule suivante comme un array, les valeurs \(1\) symbolisant la présence d’un bateau. Vous devez programmer une fonction shoot qui :

• prend en input une coordonnée \(x\) (indice de la ligne) et une cordonnée \(y\) (indice de la colonne)

• teste si au moins une valeur \(1\) est présente dans la grille :

  • si oui :

    • s’il y a un bateau à l’adresse (x, y), remplacer la valeur \(1\) par \(2\) et print “Touché !”

    • sinon, print “Raté !”

  • si non :

    • print “Fin de partie !”

Puis réalisez quelques tests pour vous assurer que votre fonction marche comme attendu.

X = np.array([[1, 1, 1, 0, 0], [0, 0, 0, 0, 1], [1, 0, 0, 0, 1],
              [1, 0, 0, 0, 0], [0, 1, 1, 1, 1]])
print(X)

[[1 1 1 0 0]
 [0 0 0 0 1]
 [1 0 0 0 1]
 [1 0 0 0 0]
 [0 1 1 1 1]]

# Testez votre réponse dans cette cellule

Afficher la solution

X = np.array([[1, 1, 1, 0, 0], [0, 0, 0, 0, 1], [1, 0, 0, 0, 1],
              [1, 0, 0, 0, 0], [0, 1, 1, 1, 1]])

def shoot(x, y):
    if np.any(X == 1):
        if X[x, y] == 1:
            print("Touché !")
            X[x, y] = 2
        else:
            print("Raté !")
        print(X)
        print()
    else:
        print("Fin de partie !")

shoot(0, 1)
shoot(1, 0)
shoot(0, 2)

One Hot Encoding

En statistique, il est fréquent de vouloir encoder numériquement un vecteur de catégories. Une manière fréquente d’encoder des catégories est le one hot encoding (OHE) : chaque valeur est représentée par un vecteur binaire, qui contient un \(1\) sur la colonne correspondant à la catégorie et des \(0\) partout ailleurs.

Dans la cellule suivante, on encode des PCS au format OHE grâce à une fonction du package scikit-learn. L’objectif de l’exercice est de reproduire cet encodage en utilisant uniquement des fonctions de la librairie NumPy.

Indice : on pourra utiliser les fonctions np.unique, np.zeros et np.arange.

from sklearn.preprocessing import OneHotEncoder

values = np.array(["21", "46", "47", "23", "66", "82", "82"])

print(OneHotEncoder().fit_transform(values.reshape((-1, 1))).todense())

[[1. 0. 0. 0. 0. 0.]
 [0. 0. 1. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0.]
 [0. 1. 0. 0. 0. 0.]
 [0. 0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 0. 1.]
 [0. 0. 0. 0. 0. 1.]]

# Testez votre réponse dans cette cellule

Afficher la solution

values = np.array(["21", "46", "47", "23", "66", "82", "82"])

categories, pos = np.unique(values, return_inverse=True)
n_values = values.shape[0]
n_categories = categories.shape[0]

ohe = np.zeros((n_values, n_categories))
ohe[np.arange(n_values), pos] = 1
ohe