Skip to contents

Appliquer la méthode des clés aléatoires

Source: vignettes/utiliser-ckm.Rmd
utiliser-ckm.Rmd

Le package contient un jeu de données pour s’exercer:

data("dtest", package = "ckm")

Une étape préalable: poser les clés individuelles

La fonction build_individual_keys() ajoute à votre jeu de données une colonne rkey contenant les clés individuelles qui sont des nombres aléatoires tirés selon une loi uniforme entre 0 et 1.

set.seed(451919)
dtest_avec_cles <- build_individual_keys(dtest)

On peut vérifier que la distribution des clés individuelles est bien uniforme.

hist(dtest_avec_cles$rkey)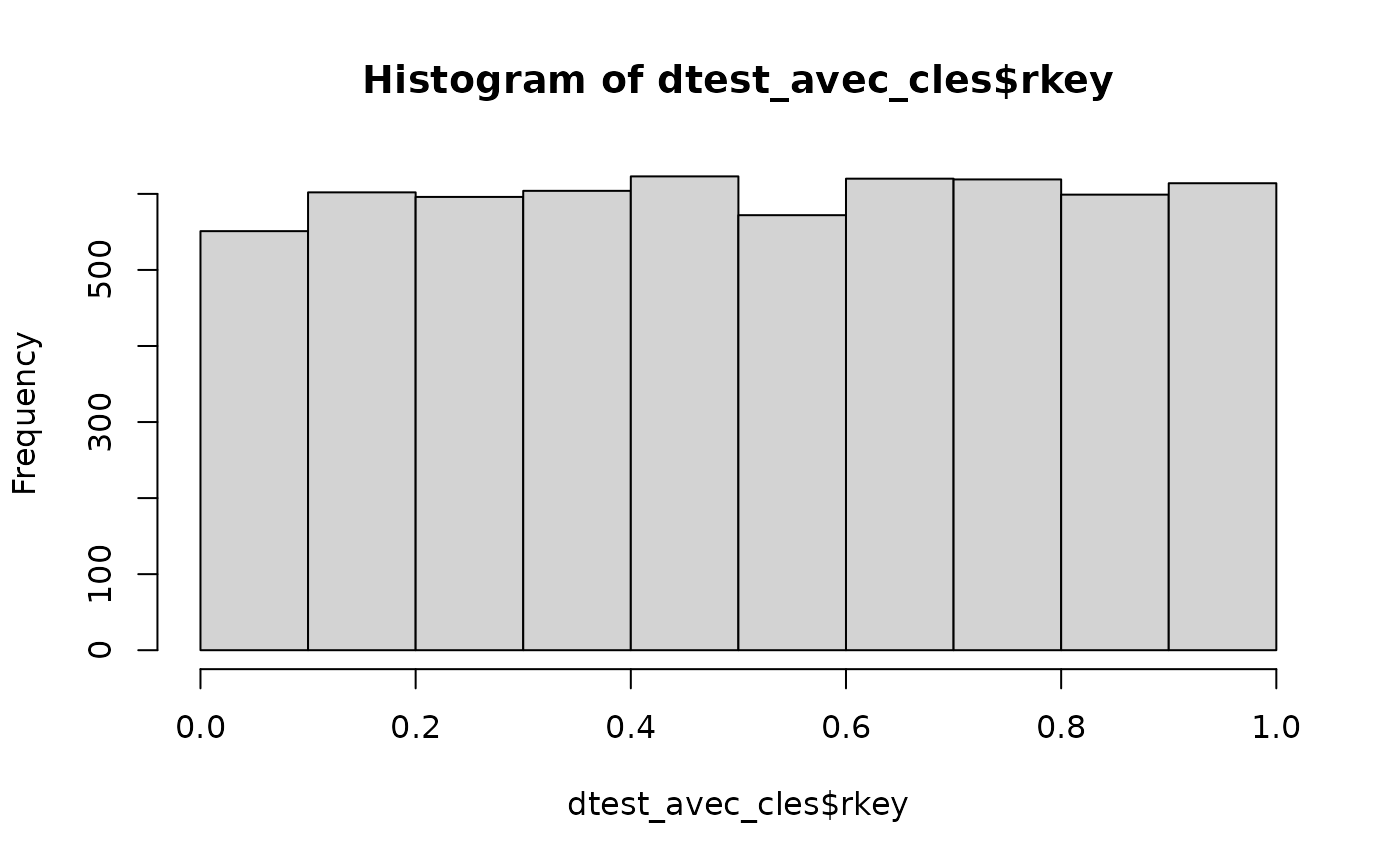

Appliquer la méthode des clés aléatoires en une étape

Après avoir généré la clé individuelle sur votre jeu de données, il est possible de construire directement le tableau perturbé.

Le code ci-dessous va réaliser les étapes suivantes:

  • construire le tableau agrégé croisant les variables "REG", "DEP","DIPLOME", "SEXE", "AGE", y compris les marges du tableau.
  • calculer la table de pertubation en fonction des paramètres D (déviation maximale) et V (la variance de la distribution)
  • appliquer la perturbation sur le tableau agrégé.
res_ckm <- tabulate_and_apply_ckm(
 df = dtest_avec_cles,
 cat_vars = c("DEP","DIPLOME", "SEXE", "AGE"),
 D = 5, V = 2
)

Le résultat renvoyé est une liste de deux éléments:

str(res_ckm, max.level = 2)
#> List of 4
#>  $ tab    : tibble [3,847 × 6] (S3: tbl_df/tbl/data.frame)
#>  $ risque : NULL
#>  $ utilite: tibble [1 × 3] (S3: tbl_df/tbl/data.frame)
#>  $ ptab   :Formal class 'ptable' [package "ptable"] with 8 slots

Appliquer la méthode des clés aléatoires étape par étape

1-Générer le tableau de comptages avec la clé des cellules

La deuxième étape consiste à construire votre tableau de comptage. Il faut pour cela renseigner le jeu de données contenant la colonne avec les clés individuelles et les variables catégorielles que vous souhaitez croiser ensemble.

La fonction tabulate_cnt_micro_data s’occupe de construire l’ensemble des croisements possibles - y compris les marges - et de fournir à la fois le comptage (le nombre d’individus contenu dans chaque croisement) et la clé de la cellule obtenue en récupérant la partie décimale de la somme des clés individuelles.

tab_avant <- tabulate_cnt_micro_data(
 df = dtest_avec_cles,
 cat_vars = c("DEP","DIPLOME", "SEXE", "AGE")
)

L’argument marge_label permet de renseigner la modalité des marges (par défaut "Total") et l’argument hrc_vars permet de renseigner une éventuelle hiérarchie entre des variables - dans le cas où vous souhaitez que cette hiérarchie apparaisse dans une unique colonne.

2-Appliquer la perturbation

La troisième étape consiste à appliquer la perturbation à la table précédente. Il suffit de renseigner, a minima :

  • le tableau sur lequel appliqué la perturbation
  • et les deux paramètres principaux de la CKM:
    • la déviation maximale D. Par exemple, D=5 conduit à dévier les données d’un entier compris entre -5 et +5.
    • la variance V de la distribution de probabilités. Plus la variance sera importante, plus la perturbation globale (mesurée par exemple par la moyenne des écarts absolus) le sera.
res_ckm <- apply_ckm(tab_avant, D = 5, V = 2)
str(res_ckm, max.level = 2)
#> List of 4
#>  $ tab    : tibble [3,847 × 6] (S3: tbl_df/tbl/data.frame)
#>  $ risque : NULL
#>  $ utilite: tibble [1 × 3] (S3: tbl_df/tbl/data.frame)
#>  $ ptab   :Formal class 'ptable' [package "ptable"] with 8 slots