1 Guide d’usage du gradient boosting

Ce guide propose des recommandations sur l’usage des algorithmes de gradient boosting disponibles dans la littérature, notamment Bentéjac, Csörgő, and Martínez-Muñoz (2021) et Probst, Boulesteix, and Bischl (2019). Contrairement aux forêts aléatoires, la littérature méthodologique sur l’usages des algorithmes de gradient boosting est assez limitée et relativement peu conclusive. Ce guide comporte un certain nombre de choix méthodologiques forts, comme les implémentations recommandées ou la procédure d’optimisation des hyperparamètres, et d’autres choix pertinents sont évidemment possibles. C’est pourquoi les recommandations de ce guide doivent être considérées comme un point de départ raisonnable, pas comme un ensemble de règles devant être respectées à tout prix.

1.1 Quelle implémentation utiliser?

Il existe quatre implémentations du gradient boosting: XGBoost, LightGBM, CatBoost et scikit-learn. Elles sont toutes des variantes optimisées de l’algorithme de Friedman (2001) et ne diffèrent que sur des points mineurs. De multiples publications les ont comparées, à la fois en matière de pouvoir prédictif et de rapidité d’entraînement (voir notamment Bentéjac, Csörgő, and Martínez-Muñoz (2021), Alshari, Saleh, and Odabaş (2021) et Florek and Zagdański (2023)). Cette littérature a abouti à trois conclusions. Premièrement, les différentes implémentations présentent des performances très proches (le classement exact variant d’une publication à l’autre). Deuxièmement, bien optimiser les hyperparamètres est nettement plus important que le choix de l’implémentation. Troisièmement, le temps d’entraînement varie beaucoup d’une implémentation à l’autre, et LightGBM est sensiblement plus rapide que les autres. Dans la mesure où l’optimisation des hyperparamètres est une étape à la fois essentielle et intense en calcul, l’efficacité computationnelle apparaît comme un critère majeur de choix de l’implémentation. C’est pourquoi le présent document décrit et recommande l’usage de LightGBM. Ceci étant, les trois autres implémentations peuvent également être utilisées, notamment si les données sont de taille limitée.

Par ailleurs, chacune de ces implémentations propose une interface de haut niveau compatible avec scikit-learn. Il est vivement recommandé d’utiliser cette interface car elle minimise les risques d’erreur, facilite la construction de modèles reproductibles et permet d’utiliser l’ensemble des outils proposés par scikit-learn.

1.2 Les hyperparamètres clés du gradient boosting

Cette section décrit en détail les principaux hyperparamètres des algorithmes de gradient boosting listés dans le tableau 1. Les noms des hyperparamètres sont ceux utilisés dans LightGBM. Les hyperparamètres portent généralement le même nom dans les autres implémentations; si ce n’est pas le cas, il est facile de s’y retrouver en lisant attentivement la documentation.

Table 1: Les principaux hyperparamètres de LightGBM
Hyperparamètre Description Valeur par défaut
objective Fonction de perte utilisée Variable
n_estimators ou num_trees Nombre d’arbres 100
learning_rate ou eta Taux d’apprentissage 0.1
max_depth Profondeur maximale des arbres -1 (pas de limite)
num_leaves Nombre de feuilles terminales des arbres 31
min_child_samples Nombre minimal d’observations qu’une feuille terminale doit contenir 20
min_child_weight Poids minimal qu’une feuille terminale doit contenir 0.001
lambda ou lambda_l2 Pénalisation quadratique sur la valeur des feuilles terminales 0
reg_alpha ou lambda_l1 Pénalisation absolue (L1) sur la valeur des feuilles terminales 0
min_split_gain Gain minimal nécessaire pour diviser un noeud 0
bagging_fraction Taux d’échantillonnage des données d’entraînement (utilisé uniquement si bagging_freq ) > 0 1
bagging_freq Fréquence de rééchantillonnage des données d’entraînement (utilisé uniquement si bagging_fraction ) < 1 1
feature_fraction Taux d’échantillonnage des colonnes par arbre 1
feature_fraction_bynode Taux d’échantillonnage des colonnes par noeud 1
max_bin Nombre de bins utilisés pour discrétiser les variables continues 255
max_cat_to_onehot Nombre de modalités en-deça duquel LightGBM utilise le one-hot-encoding 4
max_cat_threshold Nombre maximal de splits considérés
dans le traitement des variables catégorielles		 32
sample_weight Pondération des observations dans les données d’entraînement 1
scale_pos_weight Poids des observations de la classe positive (classification binaire uniquement) Aucun
class_weight Poids des observations de chaque classe (classification multiclasse uniquement) Aucun
Attention aux alias!

Il arrive fréquemment que les hyperparamètres des algorithmes de gradient boosting portent plusieurs noms. Par exemple dans LightGBM, le nombre d’arbres porte les noms suivants: num_iterations, num_iteration, n_iter, num_tree, num_trees, num_round, num_rounds, nrounds, num_boost_round, n_estimators et max_iter (ouf!). C’est une source récurrente de confusion, mais il est facile de s’y retrouver en consultant la page de la documentation sur les hyperparamètres, qui liste les alias:

Voici une présentation des principaux hyperparamètres et de leurs effets sur les performances sur le modèle de gradient boosting:

  • La mécanique du gradient boosting est contrôlée par seulement trois hyperparamètres (tous les autres hyperparamètres portant sur la construction des arbres pris isolément):

    • L’hyperparamètre objective définit à la fois la nature du problème modélisé (régression, classification…) et la fonction de perte utilisée lors de l’entraînement du modèle. La valeur par défaut varie selon le modèle utilisé: regression_l2 (minimisation de l’erreur quadratique moyenne) pour la régression, binary_log_loss (maximisation de la log-vraisemblance d’un modèle logistique) pour la classification binaire et softmax (maximisation de la log-vraisemblance d’un logit multinomial) pour la classification multiclasse. Il existe de nombreuses autres possibilités, comme regression_l1 pour la régression (minimisation de l’erreur absolue moyenne)

    • le nombre d’arbres contrôle la complexité générale de l’algorithme. Le point essentiel est que, contrairement aux forêts aléatoires, la performance du gradient boosting sur les données d’entraînement croît continûment avec le nombre d’arbres sans jamais se stabiliser. Le choix du nombre d’arbres est essentiel, et doit viser un équilibre entre amélioration du pouvoir prédictif du modèle (si les arbres supplémentaires permettent au modèle de corriger les erreurs résiduelles), et lutte contre le surajustement (si les arbres supplémentaires captent uniquement les bruits statistiques et les fluctuations spécifiques des données d’entraînement). Par ailleurs, le choix du nombre d’arbres est très lié à celui du taux d’apprentissage, et il est nécessaire de les optimiser conjointement (Probst, Boulesteix, and Bischl (2019)).

    • le taux d’apprentissage (learning rate) contrôle l’influence de chaque arbre sur le modèle global; il s’agit de \(\eta\) dans l’équation REFERENCE PARTIE OVERFITTING. Cet hyperparamètre a un effet important sur la performance du modèle global (Probst, Boulesteix, and Bischl (2019)). Un taux d’apprentissage faible réduit la contribution de chaque arbre, rendant l’apprentissage plus progressif; cela évite qu’un arbre donné ait une influence trop importante sur le modèle global et contribue donc à réduire le surajustement, mais nécessite un plus grand nombre d’arbres pour converger vers une solution optimale. Inversement, un taux d’apprentissage élevé accélère l’entraînement mais peut rendre le modèle instable (car trop sensible à un arbre donné), entraîner un surajustement et/ou aboutir à un modèle sous-optimal. La règle générale est de privilégier un taux d’apprentissage faible (entre 0.01 ou 0.3). Le choix du taux d’apprentissage est très lié à celui du nombre d’arbres: plus le taux d’apprentissage sera faible, plus le nombre d’arbres nécessaires pour converger vers une solution optimale sera élevé. Ces deux hyperparamètres doivent donc être optimisés conjointement.

  • La complexité des arbres: la profondeur maximale des arbres et le nombre de feuilles terminales contrôlent la complexité des weak learners: une profondeur élevée et un grand nombre de feuilles aboutissent à des arbres complexes au pouvoir prédictif plus élevé, mais induisent un risque de surajustement. Par ailleurs, de tels arbres sont plus longs à entraîner que des arbres peu profonds avec un nombre limité de feuilles. Le nombre optimal d’arbres est très corrélé au nombre de feuilles terminales: il est logiquement plus faible quand les arbres sont complexes. Il est à noter que le nombre de feuilles terminales a un effet linéaire sur la complexité des arbres, tandis que la profondeur maximale a un effet exponentiel: un arbre pleinement développé de profondeur \(k\) comprend \(2^k\) feuilles terminales et \(2^k - 1\) splits. Augmenter la profondeur d’une unité a donc pour effet de doubler le temps d’entraînement de chaque arbre. Ces deux hyperparamètres peuvent interagir entre eux de manière complexe (voir encadré).

  • La lutte contre le surajustement: ces hyperparamètres de régularisation jouent un rôle important dans le contrôle de la complexité des weak learners et contribuent à éviter le surajustement:

    • Les pénalisations tendent à réduire le poids \(w_j\) des feuilles terminales: la pénalisation quadratique réduit la valeur absolue des poids sans les annuler (il s’agit de \(\lambda\) dans l’équation donnant le poids optimal d’une feuille terminale), tandis que la pénalisation absolue élevée pousse certains poids à être nuls. La pénalisation quadratique est la plus utilisée, notamment parce qu’elle permet d’amoindrir l’influence des points aberrants.
    • Le nombre minimal d’observations par feuille terminale contrôle la taille des feuilles terminales. Une valeur faible autorise le modèle à isoler de petits groupes d’observations mais induit un risque de surajustement; inversement une valeur plus élevée limite le surajustement mais peut réduire le pouvoir prédictif.
    • Le gain minimal définit la réduction minimale de la perte requise pour qu’un nœud soit divisé (il s’agit du paramètre \(\gamma\) dans l’équation donnant le gain potentiel d’un split); une valeur plus élevée contribue à réduire la complexité des arbres et à limiter le surajustement en empêchant l’algorithme de créer des splits dont l’apport est très faible et potentiellement dû à des variations non significatives des données d’entraînement.

  • Les hyperparamètres d’échantillonnage:

    • le taux d’échantillonnage des données d’entraînement et le taux d’échantillonnage des colonnes par noeud jouent exactement le même rôle que sample.fraction ou max_samples, et mtry dans une forêt aléatoire: échantillonner les données d’entraînement accélère l’entraînement, et échantillonner les colonnes au niveau de chaque noeud aboutit à des arbres plus variés. Il est à noter que l’échantillonnage des données se fait systématiquement sans remise dans les algorithmes de gradient boosting. Comme pour la forêt aléatoire, la valeur optimale du taux d’échantillonnage des colonnes par noeud dépend du nombre de variables réellement pertinentes dans les données, et une valeur plus élevée est préférable si les données comprennent un grand nombre de variables binaires issues du one-hot-encoding des variables catégorielles.
    • L’échantillonnage des colonnes par arbre sert essentiellement à accélérer l’entraînement. Si les colonnes sont échantillonnées à la fois par arbre et par noeud, alors le taux d’échantillonnage final est le produit des deux taux.

  • Les réglages relatifs au retraitement des colonnes:

    • le nombre de bins utilisés pour discrétiser les variables continues (voir partie PREPROCESSING pour le détail): un faible de bins contribue à accélérer l’entraînement (car le nombre de splits potentiels est faible), mais peut dégrader le pouvoir prédictif si de faibles variations de la variable continue ont un impact notable sur la variable-cible. Inversement, une valeur élevée permet de conserver davantage d’information sur la distribution de la variable continue, mais peut ralentir l’entraînement.
    • le nombre de modalités en-deça duquel les variables catégorielles font l’objet d’un one-hot-encoding et le nombre maximal de splits considérés dans le traitement des variables catégorielles définissent la méthode utilisée pour traiter les variables catégorielles (voir partie PREPROCESSING pour le détail).

  • Les pondérations:

    • la pondération des observations sert à pondérer les données d’entraînement (voir PARTIE USAGE AVANCE).
    • le poids des observations de la classe positive sert à rééquilibrer les données d’entraînement lorsque la classe positive est sous-représentée. Cet hyperparamètre ne sert que pour la classification binaire. Par défaut les deux classes ont le même poids.
    • le poids des observations de chaque classe sert à rééquilibrer les données d’entraînement lorsque la part des différentes classes est hétérogène. Cet hyperparamètre ne sert que pour la classification binaire multiclasse. Par défaut toutes les classes ont le même poids.
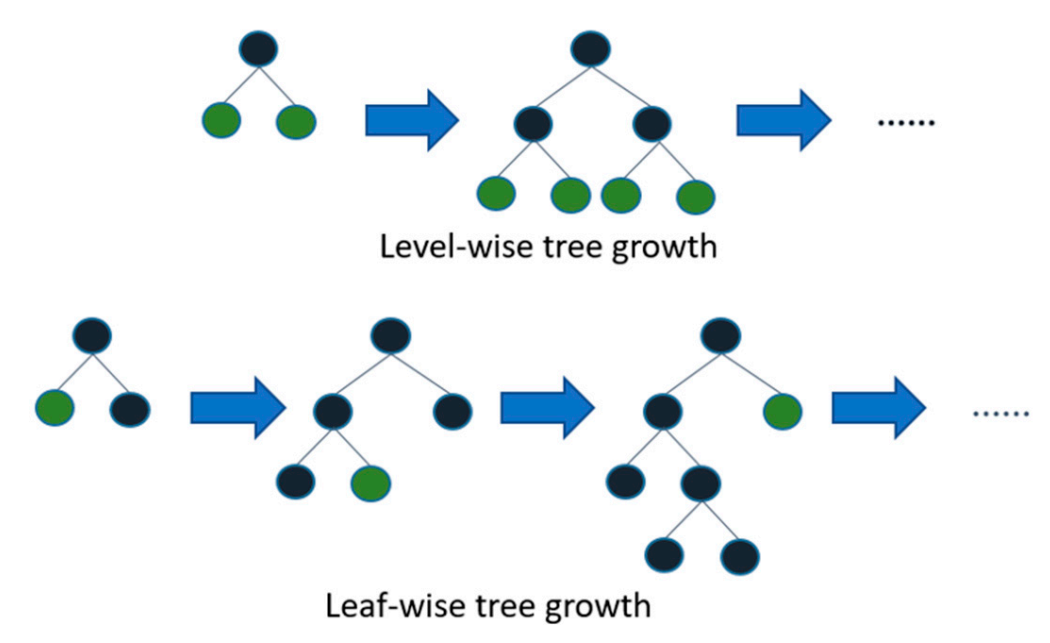
Depth-wise versus leaf-wise: les deux approches de la construction des arbres

Il existe deux méthodes de construction des arbres, illustrée par la figure ci-dessous:

  • dans l’ approche par niveau (dite depth-wise) proposée à l’origine par XGBoost, l’arbre est construit niveau par niveau, en divisant tous les nœuds du même niveau avant de passer au niveau suivant. L’approche depth-wise n’est pas optimale pour minimiser la fonction de perte, car elle ne recherche pas systématiquement le split le plus performant, mais elle permet d’obtenir des arbres équilibrés et de profondeur limitée. L’hyperparamètre-clé de cette approche est la profondeur maximale des arbres (max_depth).

  • dans l’ approche par feuille (dite leaf-wise) proposée à l’origine par LightGBM, l’arbre est construit feuille par feuille, et c’est le split avec le gain le plus élevé qui est retenu à chaque étape, et ce quelle que soit sa position dans l’arbre. L’approche leaf-wise est très efficace pour minimiser la fonction de perte, car elle privilégie les splits les plus porteurs de gain. L’hyperparamètre-clé de cette approche est le nombre maximal de feuilles terminales (num_leaves). Il se trouve que l’approche leaf-wise a été ajoutée par la suite à XGBoost, via l’hyperparamètre grow_policy qui peut prendre les valeurs depthwise (valeur par défaut) et lossguide (approche leaf-wise).

Si elle est en général plus performante que l’approche par niveau, l’approche par feuille peut aboutir à un modèle surajusté et difficile à utiliser car composé d’arbres complexes, déséquilibrés et très profonds1. Par exemple, si on fixe num_leaves à 256, on peut aisément obtenir un arbre avec une branche de profondeur 30. Il est donc important de spécifier à la fois num_leaves et max_depth lorsqu’on utilise l’approche par feuille, de façon à obtenir des arbres peu déséquilibrés. Une approche simple consiste à fixer conjointement les deux hyperparamètres: si on fixe num_leaves à \(2^k\), on peut fixer max_depth à \(k+5\). Cela signifie que dans un arbre à 256 feuilles aucune branche ne pourra pas avoir une profondeur supérieure à 13.

Figure 1

1.3 Comment entraîner un algorithme de gradient boosting?

Proposer une procédure pour l’optimisation des hyperparamètres s’avère plus délicat pour les algorithmes de gradient boosting que pour les forêts aléatoires, car ces algorithmes comprennent un nombre beaucoup plus élevé d’hyperparamètres, et la littérature méthodologique sur leur usage pratique reste assez limitée et peu conclusive (en-dehors des nombreux tutoriels introductifs disponibles sur internet). Trois constats sont néanmoins bien établis. Premièrement, optimiser les hyperparamètres est essentiel pour la performance du modèle final. Deuxièmement, contrairement aux forêts aléatoires, les valeurs par défaut des hyperparamètres dans les différentes implémentations ne constituent le plus souvent pas un point de départ raisonnable (Bentéjac, Csörgő, and Martínez-Muñoz (2021) et Probst, Boulesteix, and Bischl (2019)), en particulier pour les hyperparamètres de régularisation dont la valeur par défaut est souvent nulle. Troisièmement, cette optimisation peut s’avérer complexe et longue, il faut donc la mener de façon rigoureuse et organisée pour ne pas perdre de temps.

Parfois, une forêt aléatoire suffit…

Avant de se lancer dans le gradient boosting, il est utile d’entraîner une forêt aléatoire selon la procédure décrite dans la section ?@sec-procedure-training-rf. Ce modèle servira de point de comparaison pour la suite, et permettra notamment de voir si le gradient boosting offre des gains de performances qui justifient le temps passé à l’optimisation des hyperparamètres.

1.3.1 Préparer l’optimisation des hyperparamètres

  • Choisir les hyperparamètres à optimiser. Le nombre élevé d’hyperparamètres fait qu’il est en pratique impossible (et inutile) des les optimiser tous, il est donc important de restreindre l’optimisation aux hyperparamètres qui ont le plus d’influence sur la performance du modèle, et d’utiliser simplement des valeurs par défaut raisonnables pour les autres hyperparamètres (voir point suivant). Sur ce point, la littérature méthodologique suggère de concentrer l’effort d’optimisation sur le nombre d’arbres, le taux d’apprentissage, la complexité des arbres (nombre de feuilles et/ou profondeur maximale) et les paramètres de régularisation. Inversement, les hyperparamètres d’échantillonnage n’ont pas réellement besoin d’être optimisés une fois qu’on a choisi une valeur par défaut raisonnable (voir Probst, Boulesteix, and Bischl (2019) et Bentéjac, Csörgő, and Martínez-Muñoz (2021)). La liste des hyperparamètres à optimiser peut évidemment varier en fonction du problème modélisé; en tout état de cause, prendre le temps d’établir cette liste est essentiel pour ne pas se perdre dans les étapes d’optimisation.

  • Définir des valeurs par défaut raisonnables. Définir les valeurs par défaut des hyperparamètres est une étape importante car elle permet de gagner du temps lors de l’optimisation des hyperparamètres. Ce choix prend du temps et doit reposer sur une bonne compréhension du fonctionnement de l’algorithme et sur une connaissance approfondie des données utilisées. Voici quelques suggestions de valeurs de départ issues de la littérature (voir notamment Bentéjac, Csörgő, and Martínez-Muñoz (2021) et Probst, Boulesteix, and Bischl (2019)); il est tout à fait possible de s’en écarter lorsqu’on pense que le problème modélisé le justifie:

    • num_leaves: entre 31 et 255;
    • max_depth: entre 8 et 12;
    • min_child_samples: entre 5 et 50;
    • min_split_gain: valeur strictement positive, commencer entre 0.1 et 1;
    • lambda: valeur strictement positive; commencer avec une valeur entre 0.5 et 2; choisir une valeur plus élevée s’il y a des valeurs aberrantes sur \(y\) ou de clairs signes de surajustement;
    • bagging_fraction : valeur strictement inférieure à 1, commencer entre 0.6 et 0.8;
    • bagging_freq : valeur entière strictement positive, commencer avec 1 ;
    • feature_fraction_bynode : valeur strictement inférieure à 1, commencer entre 0.5 et 0.7; choisir une valeur plus élevée si les données comprennent un grand nombre de variables binaires issues d’un one-hot-encoding;
    • max_bin : garder la valeur par défaut; choisir éventuellement une valeur plus élevée si la la valeur par défaut ne suffit pas à refléter la distribution des variables continues;
    • max_cat_to_onehot : garder la valeur par défaut;
    • max_cat_threshold : garder la valeur par défaut.

  • Définir la méthode d’évaluation des hyperparamètres: indépendamment de la méthode d’optimisation des hyperparamètres (grid search, random search…), deux approches sont envisageables pour évaluer les valeurs possibles des hyperparamètres: soit une validation croisée (par exemple avec la fonction GridSearchCV de scikit-learn), soit une validation simple reposant sur un unique ensemble de validation. La validation simple peut être préférable si les données utilisées sont volumineuses (au-delà de plusieurs centaines de milliers d’observations) car elle offre un gain de temps appréciable, sans nécessairement dégrader les résultats. La validation croisée est censée être plus robuste que l’utilisation d’un ensemble de validation, mais elle est coûteuse sur le plan computationnel (car il faut entraîner plusieurs fois un modèle pour chaque jeu d’hyperparamètres).

1.3.2 Optimiser les hyperparamètres

Cette section propose trois approches pour optimiser les hyperparamètres d’un algorithme de gradient boosting. Les deux premières reposent sur une validation croisée et une validation simple, associée à un grid search. La troisième est plus avancée et mobilise Optuna, un framework d’optimisation d’hyperparamètres. Aucune de ces approches ne garantit pas l’obtention d’un modèle optimal, mais elle sont relativement lisibles et permettent d’obtenir rapidement un modèle raisonnablement performant.

1.3.2.1 Approche 1: procédure itérative par validation croisée

La première approche repose sur une validation croisée. Elle peut être coûteuse sur le plan computationnel en raison du nombre de modèles à entraîner et est donc adaptée à des données peu volumineuses. Cette approche comprend quatre étapes:

  • Optimiser conjointement le nombre d’arbres et le taux d’apprentissage. Par exemple, on évalue les performances du modèle en testant les valeurs [100, 200, 500, 1000] pour le nombre d’arbres, et [0.05, 0.1, 0.15, 0.2] pour le taux d’apprentissage, avec des valeurs raisonnables pour les autres hyperparamètres. On retient finalement le taux d’apprentissage et le nombre d’arbres du modèle le plus performant. Si l’un de ces hyperparamètres est la valeur minimale ou maximale testée (par exemple 1000 arbres, ou 0.05 pour le taux d’apprentissage), alors il est préférable de recommencer l’exercice en ajustant la liste des valeurs possibles.

  • Optimiser conjointement les hyperparamètres contrôlant la structure des arbres. On utilise le taux d’apprentissage et le nombre d’arbres issus de l’étape précédente, puis on évalue les performances de différents couples de valeurs (max_depth, min_child_samples), et on retient enfin les valeurs des hyperparamètres du modèle le plus performant.

  • Optimiser conjointement les hyperparamètres de régularisation. On utilise les valeurs des hyperparamètres issues des étapes précédentes, puis on évalue les performances de différents couples de valeurs (lambda, min_split_gain), et on retient les valeurs des hyperparamètres du modèle le plus performant.

  • Entraîner le modèle final avec les hyperparamètres finaux.

Utiliser l’option return_train_score = True de GridsearchCV pour mesurer le surajustement, et durcir les hyperparamètres de régularisation quand il est important.

Cette procédure est présentée en détail dans la partie 1 du notebook XXXXXXXXXXXXXXXXXXXXXXXXXXXX.

1.3.2.2 Approche 2: approche itérative par validation simple

La seconde approche est moins exigeante sur le plan computationnel, et est donc plus adaptée à des données volumineuses. Elle est très similaire à la première, et s’en distingue sur deux points. D’une part, elle repose sur une validation simple, ce qui réduit le nombre de modèles à entraîner. D’autre part, le nombre optimal d’arbres n’est pas fixé à l’avance, mais est défini à chaque étape de l’optimisation des hyperparamètres par un mécanisme d’early stopping. Celui-ci fonctionne de la façon suivante: on définit un nombre d’arbres très élevé (par exemple 50 000) et pour chaque jeu d’hyperparamètres, on laisse l’entraînement se prolonger jusqu’à ce que les performances mesurées sur l’ensemble de validation cessent de s’améliorer. Le nombre d’arbres retenu est celui pour lequel la performance sur l’ensemble de validation est maximale.

Cette procédure comprend quatre étapes:

  • Optimiser le taux d’apprentissage. On recherche un taux d’apprentissage optimal parmi une liste de valeurs (exemple: [0.05, 0.1, 0.15, 0.2]), avec des valeurs raisonnables pour les autres hyperparamètres, en entraînant le modèle sur les données d’entraînement avec un mécanisme d’early stopping utilisant l’ensemble de validation. On retient finalement le taux d’apprentissage du modèle le plus performant sur l’ensemble de validation. Si le taux d’apprentissage optimal est la valeur minimale ou maximale testée, il est préférable de recommencer l’exercice en ajustant la liste des valeurs possibles.

  • Optimiser conjointement les hyperparamètres contrôlant la structure des arbres. On utilise le taux d’apprentissage issu de l’étape précédente, puis on évalue les performances de différents couples de valeurs (max_depth, min_child_samples), et on retient enfin les valeurs des hyperparamètres du modèle le plus performant sur l’ensemble de validation.

  • Optimiser conjointement les hyperparamètres de régularisation. On utilise les valeurs des hyperparamètres issues des étapes précédentes, puis on évalue les performances de différents couples de valeurs (lambda, min_split_gain), et on retient les valeurs des hyperparamètres du modèle le plus performant sur l’ensemble de validation.

  • Entraîner le modèle final avec les hyperparamètres finaux.

Cette approche est présentée en détail dans la partie 2 du notebook XXXXXXXXXXXXXXXXXXXXXXXXXXXX.

1.3.2.3 Approche 3: utiliser Optuna

La troisième approche est plus avancée et mobilise Optuna, une librairie d’optimisation automatique des hyperparamètres des modèles de machine learning qui permet d’optimiser conjointement une liste d’hyperparamètres. L’usage d’Optuna s’avère très simple: l’utilisateur définit le modèle, la mesure de performance selon laquelle qu’il souhaite optimiser les hyperparamètres ainsi que l’espace des valeurs que ceux-ci peuvent prendre (exemple: learning_rate entre 0.01 et 0.3, num_leaves entre 30 et 1000…). Optuna tire aléatoirement un jeu d’hyperparamètres, entraîne le modèle avec ces hyperparamètres, mesure la performance obtenue et utilise cette information pour guider les essais suivants. Optuna est conçu pour converger rapidement vers les sous-espaces les plus prometteurs, et pour interrompre automatiquement les essais insuffisamment performants. Optuna garde la trace des différents essais réalisés et propose des visualisations commodes.

Cette procédure est présentée en détail dans la partie 3 du notebook XXXXXXXXXXXXXXXXXXXXXXXXXXXX.

1.4 Utiliser un modèle de gradient boosting en prédiction

La dernière étape de l’usage d’un modèle de gradient boosting consiste à l’utiliser en prédiction. Cette étape peut sembler simple au premier abord: ne suffit-il pas d’utiliser les fonctions de prédiction de l’implémentation retenue? C’est effectivement le cas, mais l’usage de ces modèles en prédiction peut buter sur un problème de performance car si les implémentations du gradient boosting sont optimisées pour être très performantes au cours de l’entraînement des modèles, elles ne le sont pas nécessairement lorsqu’on les utilise en prédiction. Cela ne pose généralement pas de problème lorsque la prédiction porte sur des données de taille restreinte, et que les modèles restent légers (arbres peu nombreux et peu complexes). En revanche, la prédiction peut devenir très lente voire impraticable lorsqu’on entend utiliser des modèles complexes (plusieurs milliers d’arbres) avec des données volumineuses (plusieurs millions d’observations).

Heureusement, un certain nombre de librairies open-source proposent d’optimiser des modèles déjà entraînés pour accélérer leur usage en prédiction. Par exemple, la librairie oneDAL, disponible en Python grâce au package daal4py, permet de compiler un modèle XGBoost, LightGBM et CatBoost déjà entraîné puis de l’utiliser directement avec Python, ce qui réduit considérablement le temps de prédiction sur des processeurs Intel (entre cinq et vingt fois plus rapide selon les cas). On peut également citer les librairies suivantes dont l’utilisation est plus complexe: tl2cgen, Forest Inference Library développée par Nvidia, et ONNX.

References

Alshari, Haithm, Abdulrazak Yahya Saleh, and Alper Odabaş. 2021. “Comparison of Gradient Boosting Decision Tree Algorithms for CPU Performance.” Journal of Institue Of Science and Technology 37 (1): 157–68.
Bentéjac, Candice, Anna Csörgő, and Gonzalo Martínez-Muñoz. 2021. “A Comparative Analysis of Gradient Boosting Algorithms.” Artificial Intelligence Review 54: 1937–67.
Florek, Piotr, and Adam Zagdański. 2023. “Benchmarking State-of-the-Art Gradient Boosting Algorithms for Classification.” arXiv Preprint arXiv:2305.17094.
Friedman, Jerome H. 2001. “Greedy Function Approximation: A Gradient Boosting Machine.” Annals of Statistics, 1189–1232.
Probst, Philipp, Anne-Laure Boulesteix, and Bernd Bischl. 2019. “Tunability: Importance of Hyperparameters of Machine Learning Algorithms.” Journal of Machine Learning Research 20 (53): 1–32.

Footnotes

  1. REFERENCE USAGE EN PREDICTION Voir par exemple cette discussion↩︎