Les méthodes perturbatrices
Pour données tabulées ou individuelles
Introduction
Objectifs
- Quelles sont les méthodes perturbatrices qui permettent de limiter les risques de divulgation ?
- Quelles méthodes s’appliquent aux données tabulées, lesquelles aux données individuelles ?
- De quel type de risque les méthodes nous protègent-elles?
- Quels sont les conséquences sur la perte d’information ?
Les méthodes principales à disposition
| Méthodes | ||
|---|---|---|
| Traitements | Non-Perturbatrices | Perturbatrices |
|
Avant tabulation (sur micro-données) |
Ré-échantillonnage | Injection de bruit |
| Recodage des variables | Micro-agrégation | |
| Suppression locale | Swapping (rang ou ciblé) | |
|
Après tabulation (sur données agrégées) |
Recodage des variables | Arrondis |
| Suppression de cases | Clés aléatoires | |
| Algo de confidentialité différentielle | ||
Il existe aussi une autre technique consistant à produire des données synthétiques.
Perturbatif vs suppressif
Dans quels cas préférer les méthodes perturbatrices aux méthodes suppressives?
- Prise en charge de diffusions complexes à traiter avec des méthodes suppressives:
- nombreux tableaux (diffusion industrielle),
- diffusion en plusieurs moments
- différenciation géographique ou de nomenclature
- Contrôler la perte d’utilité plus finement:
- un arbitrage possible en général en jouant sur les paramètres du bruit
- pas de suppression => une information disponible et manipulable
- Un cadre institutionnel qui autorise un tel usage
Perturbatif vs suppressif
Certaines limites des méthodes perturbatrices:
- Dans certains cas, perte de caractéristiques basiques des données (additivité dans les tableaux)
- Une perception du traitement du secret moins immédiate qu’avec le blanchiment
- Une pédagogie nécessaire vis-à-vis du public pour l’utilisation des données
- Des règles historiques de secret à revisiter car adaptées pour des méthodes suppressives
1 Les méthodes post-tabulation
Les méthodes post-tabulation
- Méthodes qui sont appliquées sur les données agrégées
- Certaines méthodes (en particulier les arrondis) sont plus adaptées aux comptages qu’aux volumes
- Perturbation de tout ou partie des tableaux selon la méthode
Quelques enjeux ?
En perturbant les données dans des tableaux:
- Faut-il tout perturber ou seulement une partie ?
- Comment assurer la cohérence entre les tableaux ?
- Faut-il préserver l’additivité au sein des tabeaux ?
En répondant à ces questions, on s’orientera vers une méthode plutôt qu’une autre.
2 Méthodes d’arrondi et apparentées
Méthodes d’arrondi et apparentées
- Arrondis déterministes
- Arrondis aléatoires
- Small Count Rounding
- Controlled Rounding
Des méthodes principalement adaptées aux tableaux de comptages.
Pour plus d’informations: https://sdctools.github.io/HandbookSDC/05-frequency-tables.html#sec-Rounding_freq (Hundepool et al. 2024)
Un exemple
Supposons le tableau de comptage suivant (en gras les informations jugées sensibles)
| Caractéristique | Nord | Ouest | Sud | Est | Total |
|---|---|---|---|---|---|
| Polluante | 6 | 14 | 1 | 7 | 28 |
| Non-Polluante | 3 | 2 | 1 | 13 | 19 |
| Total | 9 | 16 | 2 | 20 | 47 |
Arrondis déterministes ou aléatoires
Arrondir
Arrondir un comptage \(x\), c’est ramener sa valeur à un multiple de la base d’arrondi \(b\) choisie:
- Soit au multiple le plus proche (arrondi déterministe)
- => Un arrondi déterministe renvoie toujours la même valeur
- Soit, aléatoirement, à l’un des deux multiples les plus proches (arrondi aléatoire).
- L’arrondi est sans biais en choisissant les probabilités adéquates.
- Cette technique offre une meilleure protection
Exemple
\(b=10\) et \(x=23\):
- Arrondi déterministe: \(x^\prime = 20\).
- Arrondi aléatoire:
- \(x^\prime = 20\) avec probabilité de \(0.7\) ou
- \(x^\prime = 30\) probabilité de \(0.3\).
Un exemple
| Caractéristique | Nord | Ouest | Sud | Est | Total |
|---|---|---|---|---|---|
| Polluante | 5 | 15 | 0 | 5 | 30 |
| Non-Polluante | 5 | 0 | 0 | 15 | 20 |
| Total | 10 | 15 | 0 | 20 | 45 |
Arrondis des petits comptages
Small Count Rounding
Algorithme appliqué à des tableaux de données assurant:
- l’arrondi des petits comptages (cad les plus sensibles) dans une base \(b\)
- des comptages supplémentaires sont déviés pour:
- conserver l’additivité dans les tableaux
- et minimiser la perturbation globale
Technique implémentée dans le package R SmallCountRounding
Un exemple
| Caractéristique | Nord | Ouest | Sud | Est | Total |
|---|---|---|---|---|---|
| Polluante | 6 | 14 | 0 | 7 | 28 |
| Non-Polluante | 5 | 0 | 0 | 13 | 18 |
| Total | 11 | 14 | 0 | 20 | 45 |
Arrondi contrôlé
Controlled Rounding
Algorithme appliqué à des tableaux de données assurant:
- l’arrondi de tous les comptages selon une base \(b\)
- tout en assurant:
- la conservation de l’additivité dans les tableaux
- la minimisation de la somme des différences absolues entre valeurs originales et arrondies
Technique implémentée dans le logiciel Tau-ARGUS
Un exemple
| Caractéristique | Nord | Ouest | Sud | Est | Total |
|---|---|---|---|---|---|
| Polluante | 5 | 15 | 0 | 5 | 25 |
| Non-Polluante | 5 | 2 | 0 | 15 | 20 |
| Total | 10 | 15 | 0 | 20 | 45 |
3 La méthode des clés aléatoires (CKM)
La méthode des clés aléatoires
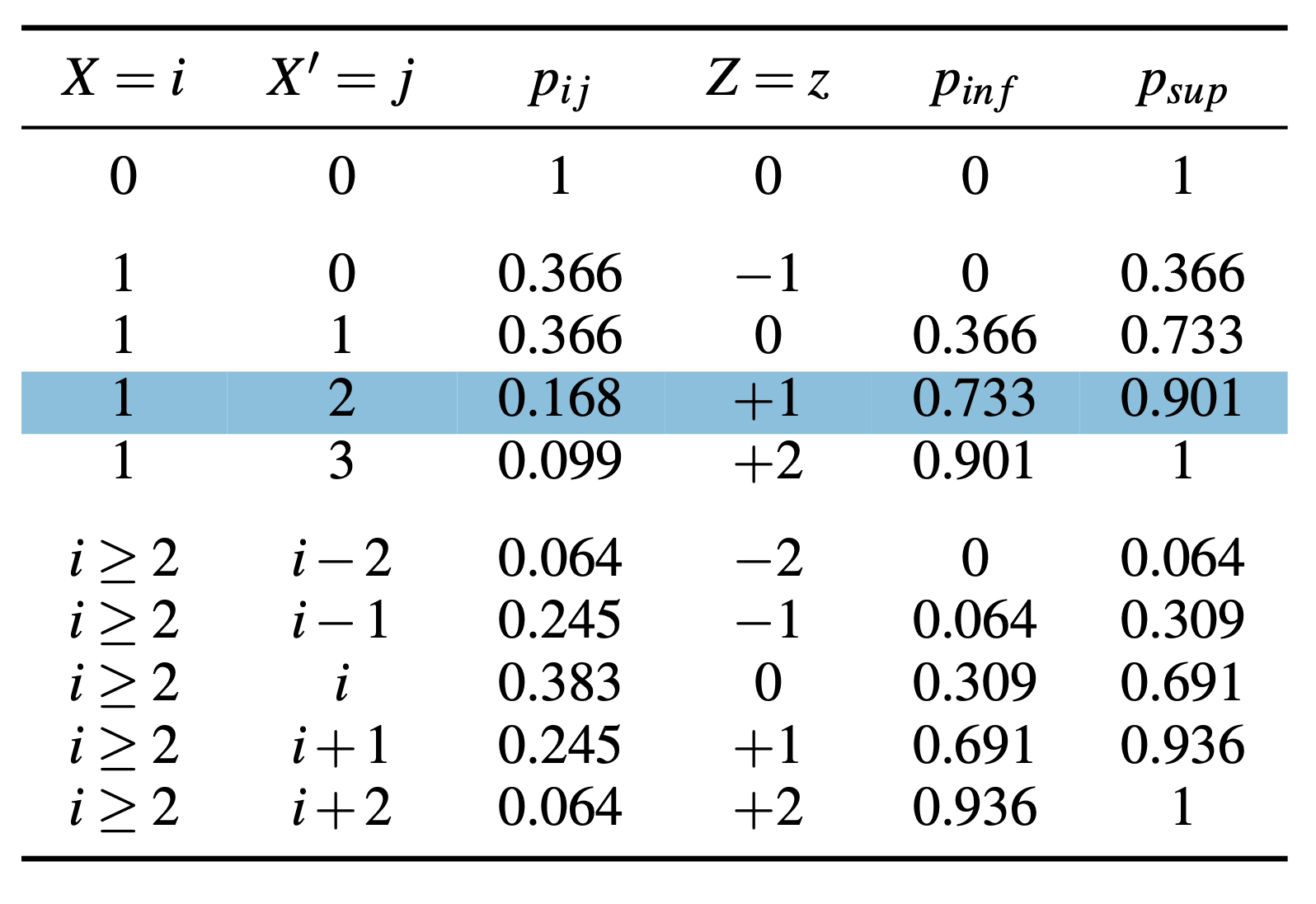
Méthode qui consiste à dévier tous les comptages indépendamment les uns des autres:
- chaque comptage est dévié d’une valeur comprise entre \(-D\) et \(+D\), \(D\) étant un paramètre de la méthode;
- une case est toujours perturbée de la même manière grâce à l’utilisation de clés individuelles
- un comptage nul n’est pas perturbé;
- la quantité de bruit injecté dans les tableaux est de variance \(V\), un autre paramètre de la méthode.
Sources: Thompson, Broadfoot, et Elazar (2013), Chipperfield, Gow, et Loong (2016), Gießing et Tent (2019)
La distribution de probabilités
Propriétés :
Une déviation maximale D et une variance V sont fixés en amont
Le bruit injecté est sans biais
La loi de probabilité de la déviation injectée est définie à partir d’une matrice de transition
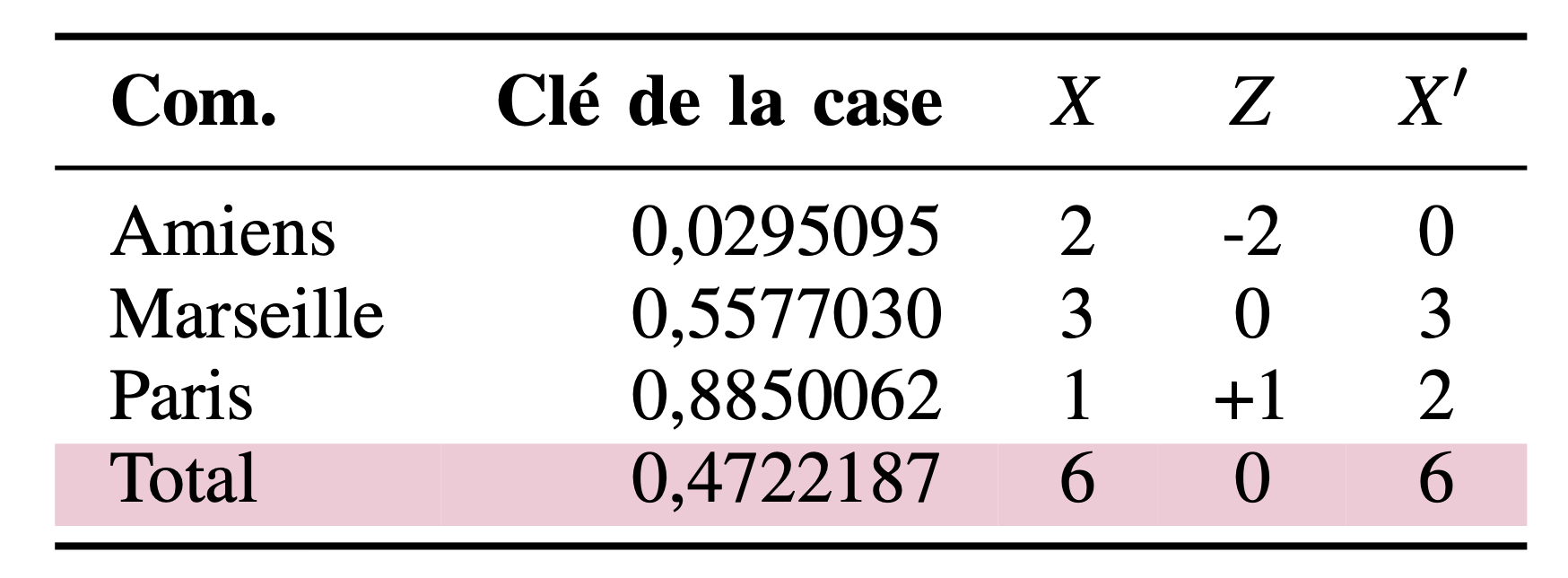
Un exemple
| Caractéristique | Nord | Ouest | Sud | Est | Total |
|---|---|---|---|---|---|
| Polluante | 4 | 15 | 0 | 8 | 28 |
| Non-Polluante | 1 | 3 | 2 | 15 | 20 |
| Total | 10 | 16 | 4 | 21 | 46 |
Les usages
La méthode est utilisée par plusieurs INS:
Depuis 2006, ABS met à disposition un outil de requêtage en ligne pour obtenir des données de son recensement quinquennal. Les données sont protégées avec la CKM. (https://tablebuilder.abs.gov.au)
La CKM est une des méthodes préconisées par Eurostat pour protéger les données du Census européen 2021.
Dans ce cadre, Destatis utilise la CKM pour diffuser des données sur des grilles de 500m.
2024/2025: l’Insee diffuse les données sur les Quartiers de la Politique de la Ville (QPV).
Etape 1: Création d’une clé individuelle aléatoire

Etape 2: Construction du tableau
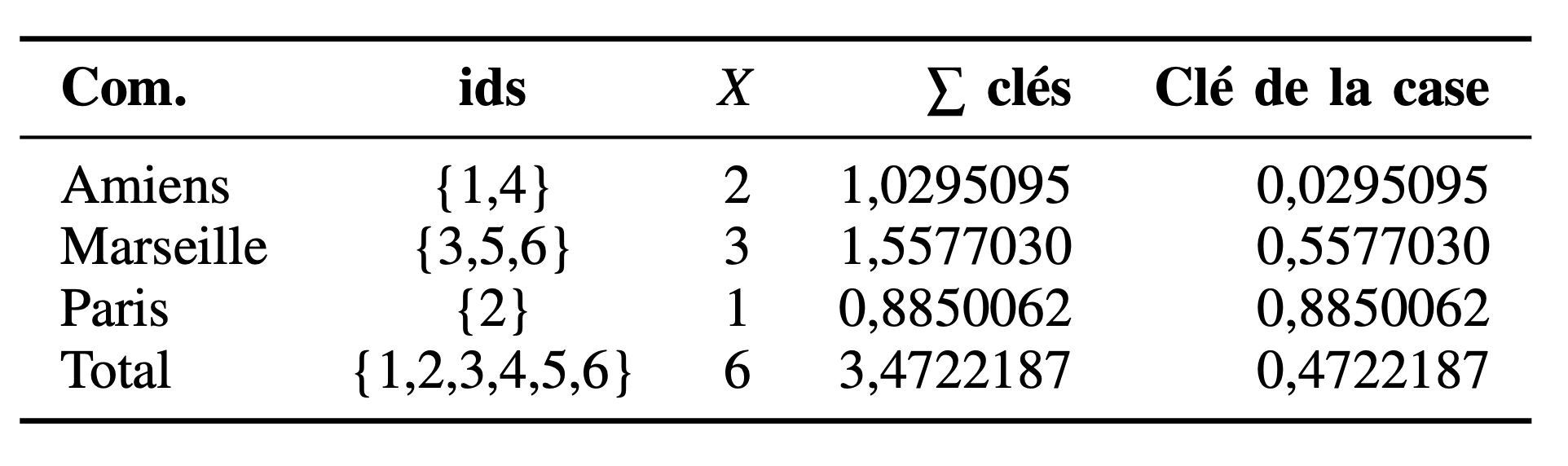
Etape 3: Les probabilités de transition
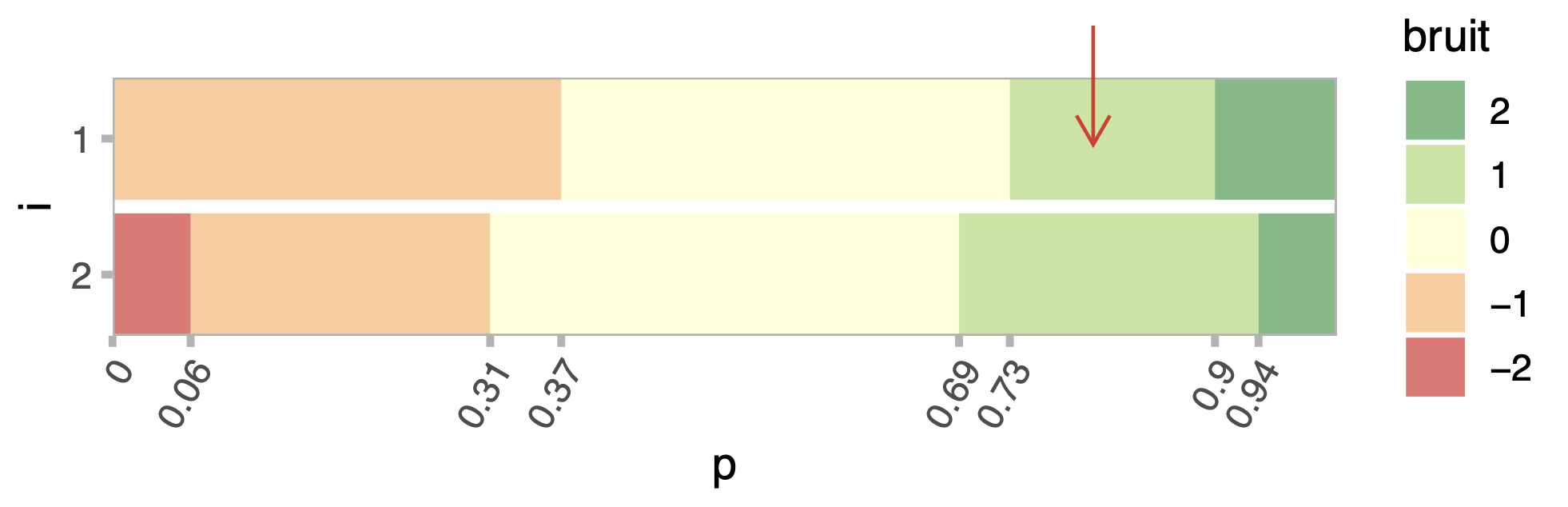
Etape 4 : Déterminer la perturbation à injecter
Etape 5 : Construire le tableau final
Avantages / inconvénients
| Avantages | Inconvénients |
|---|---|
| Facile d’implémentation | Perte de l’additivité |
| Cohérence des tableaux | Perception de gestion du secret moins facile |
| Réduit les risques de différenciation | Cumulation des bruits pour les statistiques de second ordre (ratios par ex.) |
| Compatible avec le requêtage | |
| Compatible avec une diffusion sur mesure | |
| A protection égale, meilleure utilité que les arrondis |
4 La microagrégation
Méthode perturbatrice, plus adaptée aux variables continues, mais peut-être adaptée aux variables catégorielles ordonnées
-
Idée principale :
Créer des petits groupes homogènes en prenant en compte les valeurs des variables sélectionnées
Remplacer les valeurs de tous les individus appartenant au groupe par une unique valeur (peut être la valeur moyenne de valeurs observées dans le groupe)
Un exemple
| Région | Âge | Heures travaillées par semaine | Revenu mensuel |
|---|---|---|---|
| 92 | 36 | 17 | 1000 |
| 75 | 41 | 35 | 2000 |
| 75 | 52 | 0 | 1100 |
| 94 | 45 | 35 | 2500 |
| 75 | 41 | 0 | 1900 |
| 92 | 26 | 46 | 1500 |
| 92 | 31 | 38 | 800 |
| 94 | 48 | 30 | 1200 |
Un exemple
| Région | Âge | Heures travaillées par semaine | Revenu mensuel |
|---|---|---|---|
| 92 | 17 | 1000 | |
| 75 | 35 | 2000 | |
| 75 | 0 | 1100 | |
| 94 | 35 | 2500 | |
| 75 | 0 | 1900 | |
| 92 | 46 | 1500 | |
| 92 | 38 | 800 | |
| 94 | 30 | 1200 |
- \(\mu_{red} = 45\), \(\mu_{yellow} = 31\), \(\mu_{green} = 47\)
Paramètres
Un grand nombre de sorties possibles pour cette méthode selon :
la définition d’homogénéité choisie
l’algorithme utilisé pour construire les groupes
la détermination de la valeur de remplacement
Les paramètres à définir :
Taille \(g\) de chaque groupe (plus la taille du groupe est grande, plus grande sera la perte d’information, et plus celle-ci est grande, plus le niveau de protection est élevé ..)
Quelles variables sont utilisées pour calculer la distance ?
Quelles statistiques choisir une fois que les groupes ont été formés ? (moyenne, médiane ?)
Minimiser la variance intra-groupe
L’algorithme cherche à minimiser la somme des carrés intra-groupe:
\[SSE = \sum_{i=1}^g\sum_{j \in i} (x_{ij}-\bar x_{i})^T(x_{ij}-\bar x_{i})\]
Avantages / inconvénients
| Avantages | Inconvénients |
|---|---|
| Adapté au \(k\)-anonymat | Temps de calcul important |
| Des classes statistiquement pertinentes |
5 Injection de bruit
Injection de bruit
Méthode adaptée pour traiter les variables continues
En général, on injecte un bruit additif sans biais et à variance fixe
Enjeu principal: comment bruiter en préservant les caractéristiuqes des variables et de leurs éventuels liens ?
Perturbation par un bruit additif
- Un bruit est ajouté à chaque valeur observée
- Généralement un bruit gaussien d’espérance nulle
- Adapté aux variables continues de faible amplitude
Bruits additifs indépendants
Chaque variable est bruitée indépendamment des autres variables
Les moyennes et covariances de chaque variable perturbée sont préservées
Mais, les variances et les coefficients de corrélation ne sont pas conservés
Bruits additifs corrélés
La matrice de variance-covariance des bruits est proportionnelle à la matrice de variance covariance des valeurs originales
Conservation de la moyenne et des coefficients de corrélation
Préférable à l’ajout des bruits indépendants car on peut obtenir des estimations non biaisées pour plusieurs statistiques importantes
Avantages / inconvénients
| Avantages | Inconvénients |
|---|---|
| Traitement de variables sensibles continues | Pas adapté aux traitements des outliers de grandes valeurs |
| Préservations de statistiques importantes |
6 Targeted Record Swapping (TRS)
Targeted Record Swapping (TRS)
Définition
Le Target Record Swapping (TRS) est une méthode s’appliquant directement sur un jeu de données individuelles pour réduire les risques de ré-identification.
Il consiste à échanger la localisation de certains individus jugés à risque avec d’autres individus d’une autre entité géographique.
D’où son nom: le swapping, c’est-à-dire l’échange, va concerner des unités de la base (les records) détectés à l’avance, devenant ainsi les cibles (target) sur lesquelles l’échange se concentrera.
Les individus à risque (cibles)
- Cible les individus à risque:
- Détection par \(k\)-anonymat: croisements de quasi-identifiants de moins de \(k\) individus
- Détection par \(l\)-diversité: homogénéité d’un groupe sur une variable sensible
- Mesure probabiliste du risque individuel
- Principalement un risque de ré-identification
Une méthode très utilisée
Insee: Données européennes du recensement 2021
Eurostat préconise cette méthode (couplée à la CKM) pour la diffusion du Census européen
US Census Bureau: Recensement US 2010
ONS (UK): Recensement depuis 2010
Un exemple
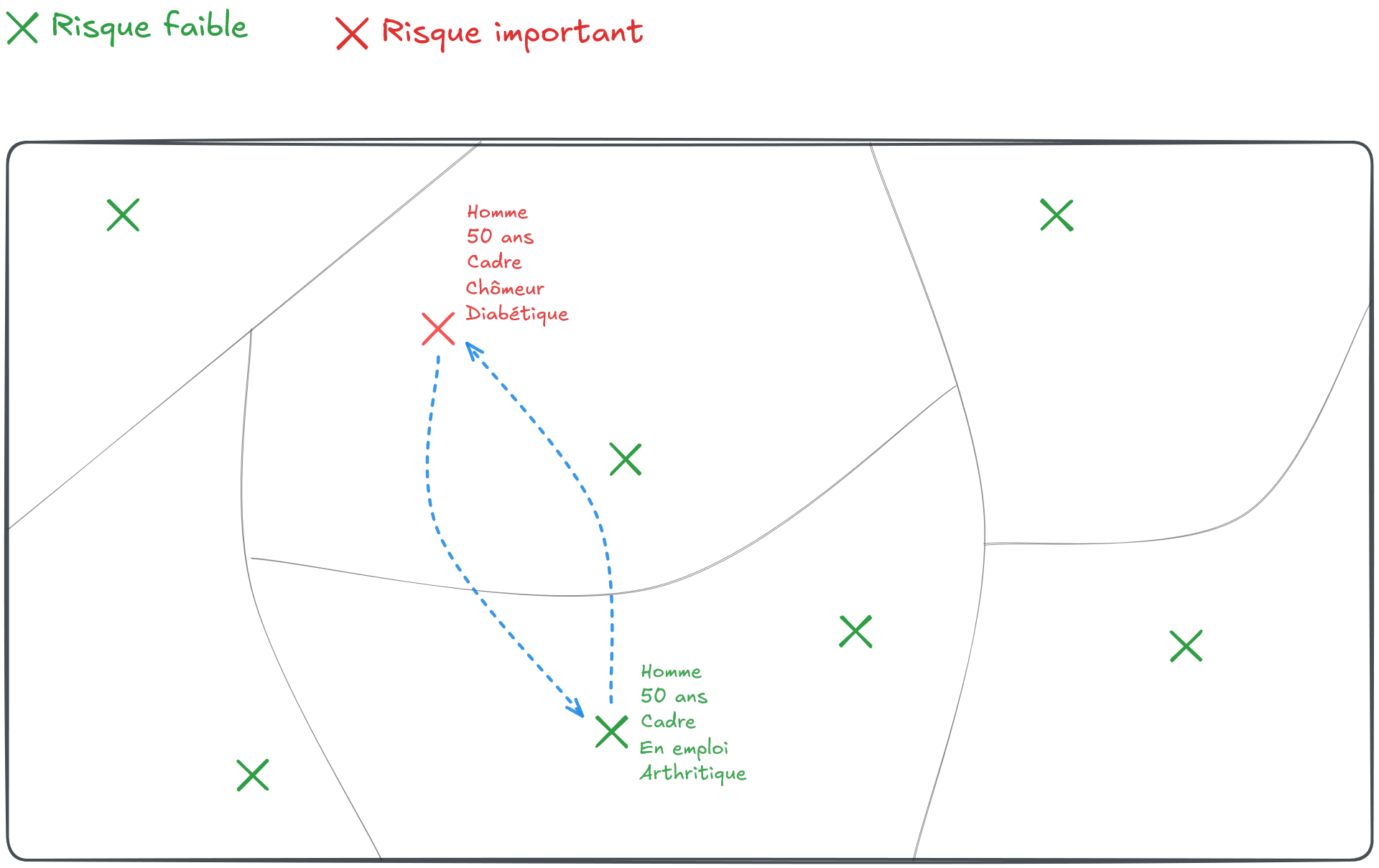
Un exemple
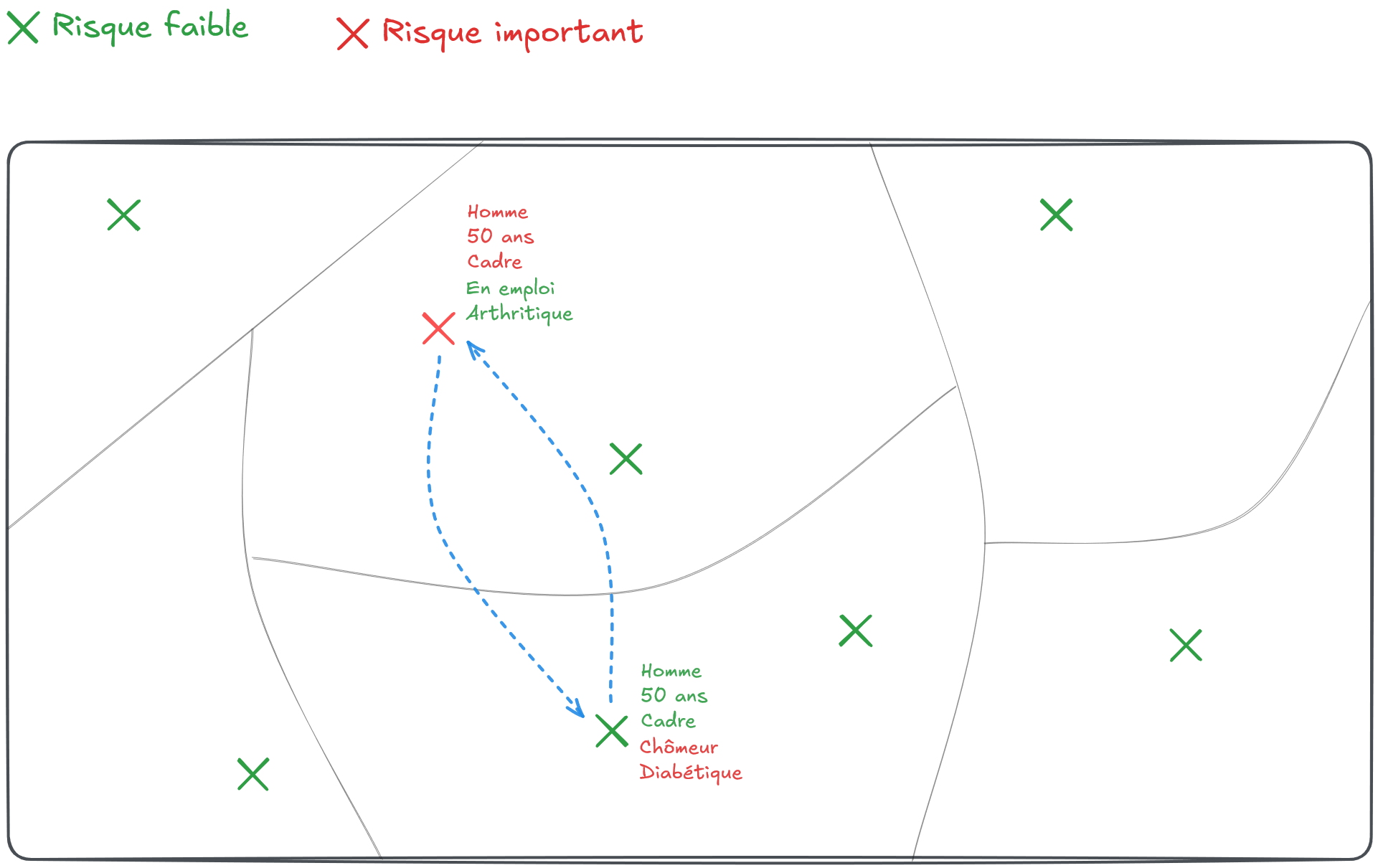
Avantages / inconvénients
| Avantages | Inconvénients |
|---|---|
| Efficace pour traiter différents types de risque | Nécessite de fixer un grand nombre de paramètres (mesure de risque, variables similarité, taux de swapping) |
| Méthode souple, adaptation à des cas très différents (structures ménages-individus par ex.) | Bruit injecté dans les données n’est pas vraiment contrôlable |
| Préserve les agrégats du niveau géographique au sein duquel le swapping a été opéré. | Génère localement du biais dans les données |
| Conserve l’additivité des tableaux générés à partir des micro-données bruitées. |
7 Post-Randomisation Method (PRAM)
Méthode PRAM
Permet de traiter les variables sensibles catégorielles en bruitant les données.
Consiste à modifier aléatoirement l’appartenance des individus à une classe donnée.
Méthode particulièrement intéressante pour traiter les divulgations d’attributs sensibles : un attaquant ne peut avoir aucune certitude sur l’attribut d’une observation.
Un exemple
| Region | Age | Situation pro. |
| 92 | 14 | Inactif |
| 75 | 41 | Chômeur |
| 75 | 52 | Actif |
| 94 | 45 | Actif |
| 75 | 41 | Chômeur |
| 92 | 26 | Actif |
| 92 | 31 | Actif |
| 94 | 14 | Inactif |
- Inactif : 2 ind., Chômeur = 2 ind., Actif = 4 ind.
Un exemple
| Region | Age | Situation pro. | Situation pro. (PRAM) |
| 92 | 14 | Inactif | Chômeur |
| 75 | 41 | Chômeur | Actif |
| 75 | 52 | Actif | Actif |
| 94 | 45 | Actif | Actif |
| 75 | 41 | Chômeur | Inactif |
| 92 | 26 | Actif | Actif |
| 92 | 31 | Actif | Chômeur |
| 94 | 48 | Inactif | Inactif |
- Inactif : 2 ind., Chômeur = 2 ind., Actif = 4 ind.
Un exemple
| Region | Age | Situation pro. | Situation pro. (PRAM) |
| 92 | 14 | Inactif | Chômeur |
| 75 | 41 | Chômeur | Actif |
| 75 | 52 | Actif | Actif |
| 94 | 45 | Actif | Actif |
| 75 | 41 | Chômeur | Inactif |
| 92 | 26 | Actif | Actif |
| 92 | 31 | Actif | Chômeur |
| 94 | 48 | Inactif | Inactif |
- Attention aux incohérences !
La matrice de transition
On a besoin de définir une matrice de transition pour pouvoir définir les probabilités de transition.
Soit \(\xi\) la variable catégorielle initiale avec \(K\) catégories \(1 \dots K\)
\(\rightarrow\) dans l’exemple, \(\xi\) = Situation professionnelle, K = 3Soit \(X\) la même variable catégorielle dans le jeu de données perturbé
\(\rightarrow\) dans l’exemple, \(X\) = Situation professionnelle (PRAM)
La matrice de transition
On peut définir la matrice de transition \(P\),
\[P =(p_{kl})_{1 \leq k,l \leq K}\]
où \(p_{kl} = P(X =l|\xi = k)\)
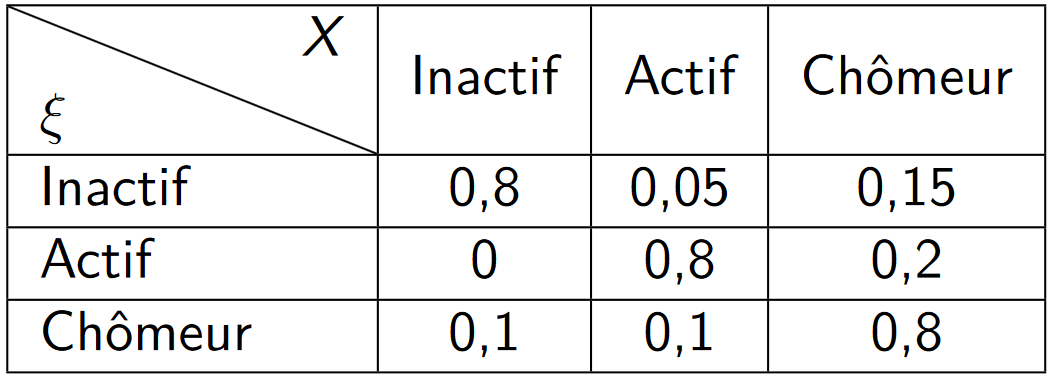
Un exemple numérique
-
Marges originales
Ina ctif Act if Chô meur Fréquence (million) 16.8 49 4.2 Pourcentage 24 % 70 % 6 % Matrice de transition \(P\) :

Un exemple numérique
On peut maintenant calculer les marges perturbées !
-
Marges originales
Statut Inactif Actif Chômeur Fréquence (million) 17 49 4 Pourcentage 24% 70% 6% -
Nouvelles marges
Statut Inactif Actif Chômeur Fréquence 14 41 16 Pourcentage 20% 58% 22 %
PRAM Invariant
Possibilité de choisir la matrice \(P\) de telle sorte que la perturbation soit sans biais \(\rightarrow\) PRAM invariant
Etant donné que : \[\mathbb{E}\begin{pmatrix} N^{pram}_{I} \\N^{pram}_{E}\\ N^{pram}_{U} \end{pmatrix} = P^{T} \begin{pmatrix}N_{I} \\N_{E}\\ N_{U} \end{pmatrix}\]
Il faut, pour cela, choisir \(P\) telle que les fréquences marginales originales soient un vecteur propre de \(P\) associé à la valeur propre \(1\).
Mesurer le niveau de protection
PRAM introduit délibérement une erreur de mesure \(\rightarrow\) on ne peut pas utilisé le k-anonymat ou la l-diversité
Niveau de protection mesuré à partir des paramètres de la méthode (matrice de transition).
Idée: faire en sorte que la rareté de certaines modalités soit rendue suffisamment incertaine à inférer \(\rightarrow\) posterior odds ratio
Mesurer le niveau de protection
\[POST\_ODDS(k) = \frac{P(\xi = k|X=k)}{P(\xi \neq k|X=k)} = \frac{p_{kk}P(\xi = k)}{\sum_{l \neq k}p_{lk}P(\xi=l)}\]
- \(p_{kk}\) sont connus et dépendent du plan de sondage
- \(P(\xi = k)\) peut être difficile à estimer
- on peut estimer grossièrement \(P(\xi = k)\) par \(\frac{T_\xi(k)}{n}\)
Interprétation
On observe k dans le jeu pertubé :
Si \(POST\_ODDS(k) > 1\), alors la valeur originale est plus probablement \(k\) plutôt qu’une autre valeur.
Si \(POST\_ODDS(k) < 1\), alors la valeur originale est plus probablement une autre valeur que \(k\).
Avantages / inconvénients
| Avantages | Inconvénients |
|---|---|
| Permet de fournir le niveau de protection associé au bruit injecté en calculant les probabilités de transition inverses | Création d’éventuelles combinaisons impossibles (ex : enfant à la retraite). |
| Conserve l’additivité des tableaux générés à partir des micro-données bruitées. | Difficile de définir une matrice de protection qui prend en compte les liens avec toutes les variables. |
8 Les données synthétiques
Idée: Générer tout ou partie des données individuelles.
-
Deux types de synthèse:
Synthèse complète: toutes les variables et tous les individus sont générés.
Synthèse partielle: Seulement certaines variables sont générées (principalement les variables sensibles).
Modélisation séquentielle
Fully Conditional Specification
Chaque variable du jeu de données est modélisée séquentiellement et conditionnellement aux variables précédentes.
Pour générer la \(p^e\) variable, on cherche à modéliser sa distribution conditionnelle :
\[f_{X_p | X_1 , X_2 , \dots , X_{p-1}}\]
Modèles statistiques couramment utilisés: - modèles paramétriques (régression linéaire ou logistique) - méthodes à base d’arbres: CART, Boosting, random forest, XGBoost.
Les méthodes Deep Learning (I)
Tabular Variational Auto Encoder (TVAE)
L’auto encodage consiste à combiner une phase d’encodage qui réduit la dimension des données pour apprendre les caractéristiques les plus importantes et une phase de décodage pour reconstituer des données dans leur dimension originale.
Les méthodes Deep Learning (II)
Conditional Tabular Generative Adversarial Network (CTGAN)
Les GAN sont très populaires dans la génération d’images. Les CTGAN sont une adaptation des GAN pour générer des données tabulaires (microdonnées ou données agrégées). Un générateur construit des données synthétiques et les soumet à un discriminateur dont l’objectif est de distinguer ces données générées des données originales.
Références
Les méthodes de protection statistique des données confidentielles
Comment choisir la matrice de transition ?
PRAM change aléatoirement les comptages de la population :
\[\mathbb{E}\begin{pmatrix} N^{pram}_{I} \\N^{pram}_{E}\\ N^{pram}_{U} \end{pmatrix} = P^{T} \begin{pmatrix}N_{I} \\N_{E}\\ N_{U} \end{pmatrix}\]
Selon P et les comptages originaux, les marges peuvent être beaucoup perturbées !
Des coefficients diagonaux élevés peuvent être insuffisants