Mesurer l’utilité
Contrôler la perte d’information
1 Définir
Quels usages des données ?
En fonction des utilisateurs finaux, le concept de perte d’information peut changer
Connaître les utilisations qui seront faites des données (ex. régression, aggrégats, moyennes)
Il n’est pas recommandé de publier plusieurs versions protégées du même jeu de données pour chaque type d’utilisateur \(\rightarrow\) risques de divulgation importants par différenciation.
Idée principale
Deux moyens de mesurer la perte d’information :
Comparer les enregistrements bruts entre le jeu de données original et le jeu de données protégé
Comparer certaines statistiques calculées sur les jeux de données originaux et protégés
2 Données continues
Notations
Pour les données continues, formellement :
\(I_1,\dots, I_n\), \(n\) enregistrements individuels
\(Z_1,..,Z_p\), \(p\) données continues
\(X\) la matrice de données originale, \(X^{'}\) la matrice de données protégée
Distance entre matrices
- Erreur quadratique moyenne : somme des différences au carré entre les deux matrices, composante par compasante, divisée par le nombre de coefficients d’une matrice (même pour les deux) \[\frac{1}{np}\sum_{j=1}^p\sum_{i=1}^n(x_{ij}-x^{'}_{ij})^2\]
Distance entre matrices
- Erreur absolue moyenne : somme des différences absolues entre les deux matrices, composante par composante, divisée par le nombre de coefficients d’une matrice (même pour les deux) \[\frac{1}{np}\sum_{j=1}^p\sum_{i=1}^n|x_{ij}-x^{'}_{ij}|\]
Distance entre matrices
- Variation moyenne : somme des variations absolues en pourcentage des composantes de la matrice protégée par rapport à la matrice de données originale \[\frac{1}{np}\sum_{j=1}^p\sum_{i=1}^n\frac{|x_{ij}-x^{'}_{ij}|}{|x_{ij}|}\]
Avec \(x_{ij} \ne 0\).
“En moyenne, chaque cellule a été modifiée de x% par rapport à la valeur d’origine.”
Un exemple
| Sexe | Rég | Âge | h / semaine |
| F | 92 | 36 | 17 |
| M | 75 | 41 | 35 |
| F | 75 | 52 | 5 |
| Sexe | Rég | Âge | h / semaine |
| F | 92 | 34 | 23 |
| F | 75 | 48 | 35 |
| M | 75 | 58 | 2 |
Un exemple
- Erreur quadratique moyenne =
\(\frac{(36-34)^2+(41-48)^2+(52-58)^2+(17-23)^2+(35-35)^2+(5-2)^2}{6}=22\)
- Erreur absolue moyenne =
\(\frac{|36-34|+|41-48|+|52-58|+|17-23|+|35-35|+|5-2|}{6}=4\)
- Variation moyenne =
\(\frac{\frac{|36-34|}{36}+\frac{|41-48|}{41}+\frac{|52-58|}{52}+\frac{|17-23|}{17}+\frac{|35-35|}{35}+\frac{|5-2|}{5}}{6}=0.15\)
Effet de taille variation moyenne
La variation moyenne dépend de la taille de \(x_{ij}\) :
\(x_{ij}\) grande \(\rightarrow\) même une différence importante \(|x_{ij} - x^{'}_{ij}|\) donne un ratio faible
\(x_{ij}\) petite \(\rightarrow\) même un petit écart absolu \(|x_{ij} - x^{'}_{ij}|\) donne un ratio élevé
Corriger l’effet de taille
Pour que le ratio ne dépende pas de la taille de \(x_{ij}\) on utilise une autre mesure : \[\frac{1}{np}\sum_{j=1}^p\sum_{i=1}^n\frac{|x_{ij}-x^{'}_{ij}|}{\sqrt{2}S_j}\] avec \(S_j\) l’écart type de la \(j\)-ème variable
Permet de comparer les variations à variabilité “normale” de la variable.
Mesures spécifiques
Comparaisons univariées (comparaison de la distribution d’une variable avant et après perturbation).
Comparaisons bivariées: Corrélations linéaires par exemple.
Comparaison multivariées: Comparaison des plans d’une analyse en composante principale.
Comparaison des paramètres d’une régression, etc.
3 Données catégorielles
Différentes comparaisons
Pour les variables catégorielles, 3 idées principales pour évaluer la perte d’information avec des données catégorielles :
-
Comparaison directe des valeurs des variables
Écarts absolus moyens
Écarts absolus relatifs moyens
Comparaison des tables de contingence
Mesures basées sur l’entropie
Mesure basée sur l’entropie
L’entropie mesure l’incertitude induite par une distribution de probabilité donnée : \[H(V|V^\prime=j) = - \sum_{i=1}^K P(V=i|V^\prime = j) \log(P(V=i|V^\prime = j))\]
Selon la méthode, il peut être difficile d’évaluer la quantité \(P(V=i|V^{'} = j)\)
Risque global \[R = \sum_{r \in enregistrements} H(V|V^\prime=\underset{valeur protégée}{\underbrace{j_{r}}})\]
Mesurer la qualité d’une inférence
- \(K = 5\) catégories, soit \(j = 4\), et examinons \(P(V=i|V^{'} = 4)_{1\leq i\leq 5}\)
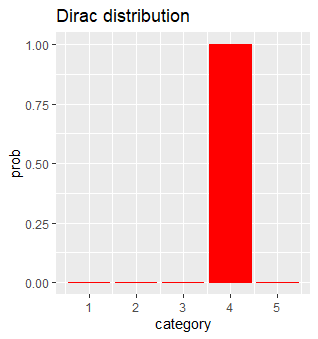
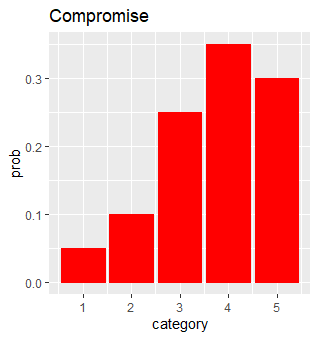

- Compromis entre risque et perte d’information !
Mesures globales
- Écarts absolus moyens ou relatifs
- Distance de Hellinger
\[HD(\mathbf{X}, \mathbf{X}') = \frac{1}{\sqrt{2}} \sqrt{\sum_{j = 1}^M \left(\sqrt{\frac{x'_j}{\sum_{j=1}^M x'_j}} - \sqrt{\frac{x_j}{\sum_{j=1}^M x_j}}\right)^2}\]
Métriques spécifiques pour tableau de contingence
- Comparaison des V de Cramer (basée sur la statistique du \(\chi^2\))
- Comparaison du 1er plan factoriel d’une analyse factorielle des correspondances.
4 S’appuyer sur la visualisation
De nombreuses possibilités
- Univarié: histogrammes, boîtes à moustaches, diagrammes en barres
- Bivarié: Matrices de corrélations, Diagrammes en mosaïques, Plan d’une analyse factorielle des correspondances, etc.
- Multivarié: 1er plan d’une analyse factorielle (ACP, ACM, AFDM)
Matrice de corrélation

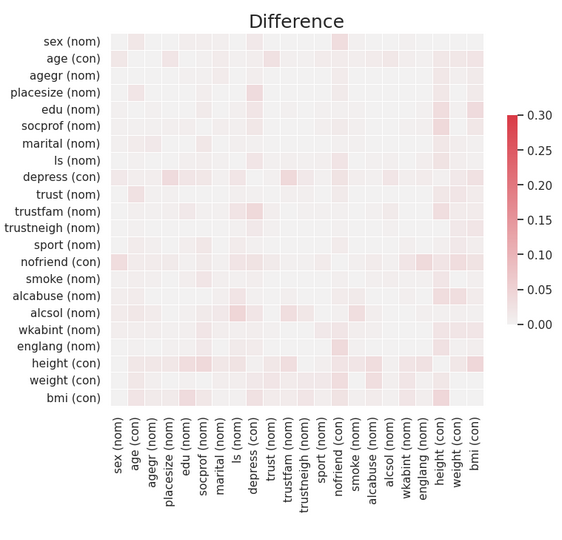
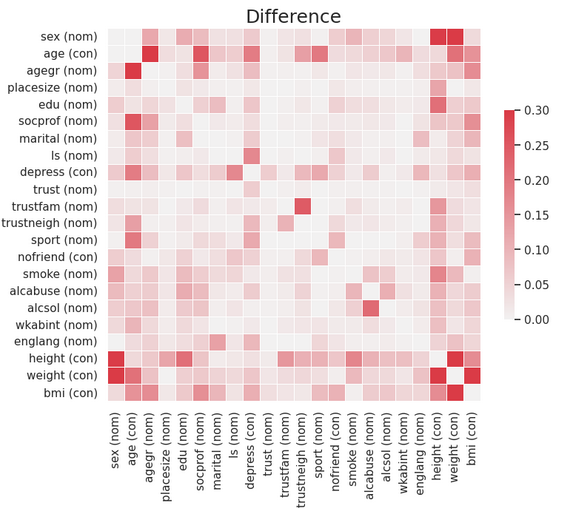
La comparaison visuelle permet immédiatement de voir que la 1ere méthode conserve mieux les relations bivariées que la 2eme.
Nuages d’une analyse factorielle
Comparaison de la projection des individus sur le premier plan d’une analyse factorielle.
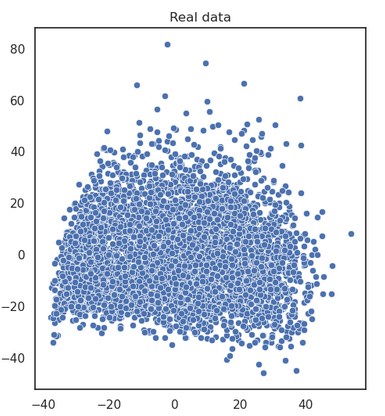
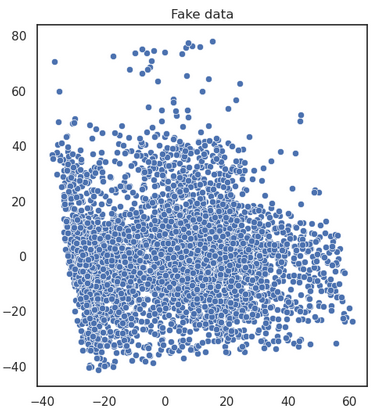
Résultats d’une régression
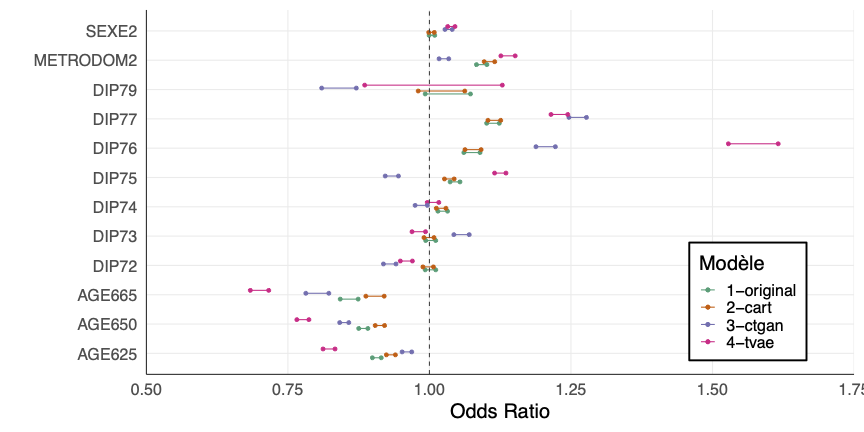
Mesurer l’utilité
Comment la définir ?