Code
library(readr)
library(purrr)
library(ggplot2)
library(dplyr)
library(sdcMicro)Insee, Département des Méthodes Statistiques
REG DEP ARR SEXE AGE AGE6 ACTEU DIP7 PCS1Q ANCCHOM HHID
<fctr> <fctr> <fctr> <fctr> <int> <fctr> <fctr> <fctr> <fctr> <fctr> <int>
1: 28 76 761 1 53 50 1 4 30 99 3558
2: 28 76 761 2 43 25 1 7 52 99 3558
3: 28 76 761 2 17 15 3 5 99 99 3558
4: 28 76 761 1 17 15 3 4 99 99 3558
5: 11 92 922 1 42 25 1 7 62 99 5973
6: 11 92 922 2 54 50 1 7 62 99 5973
HH_TAILLE HH_AGE HH_DIP HH_PCS IS_CHOM
<fctr> <fctr> <fctr> <fctr> <int>
1: 4 53 4 30 0
2: 4 53 4 30 0
3: 4 53 4 30 0
4: 4 53 4 30 0
5: 2 54 7 62 0
6: 2 54 7 62 0Dans un jeu de données, on distingue trois grands types de variables:
Ainsi, le premier type de variables engendre un risque de divulgation d’information confidentielle par la possibilité pour l’attaquant de ré-identifier des individus. En effet, si un ataquant dispose d’un fichier nomminatif - un fichier client par exemple - contenant des variables communes avec le jeu de données qu’on s’apprête à publier, il est alors en mesure d’apparier les deux et être en capacité de ré-identifier des individus si ceux-ci se trouvent avoir des caractéristiques peu fréquentes.
Prenons une liste très restreinte de quasi-identifiants: la géographie de résidence, le sexe et l’âge de l’individu. Ces informations sont disponibles par de nombreuses entreprises auprès desquelles nous souscrivons des services (banque, assurance, téléphonie, etc.).
En dénombrant les individus de chaque croisement entre les variables quasi-identifiantes, on peut détecter :
REG DEP ARR SEXE AGE n
<fctr> <fctr> <fctr> <fctr> <int> <int>
1: 11 75 751 2 97 1
2: 11 75 751 2 102 1
3: 11 75 751 2 103 1
4: 11 75 751 2 116 1
5: 11 77 771 1 15 1
6: 11 77 771 1 18 1 REG DEP ARR SEXE AGE n
<fctr> <fctr> <fctr> <fctr> <int> <int>
1: 11 75 751 2 52 43
2: 11 75 751 1 51 39
3: 11 75 751 1 21 36
4: 11 75 751 2 60 36
5: 11 75 751 2 61 36
6: 11 75 751 1 55 35Ainsi, si une entreprise de notre contrée imaginaire dispose d’un fichier sur tout ou partie de la population en âge de travailler (par exemple un opérateur téléphonique), il pourra ré-identifier sans peine les individus uniques du jeu de données qui seraient présents dans son fchier.
La capacité d’un attaquant à pouvoir ré-identifier un individu dépend du nombre d’individus du jeu de données qui partagent les mêmes caractéristiques sur les variables quasi-identifiantes.
Par exemple, si Thérèse est une femme de 97 ans résidant dans l’arrondissement 751, alors le jeu de données permet de la ré-identifier de façon certaine, puisqu’elle serait la seule dans ce cas.
Au contraire, si Thérèse est une femme de 52 ans résidant dans le même arrondissement, alors la probabilité de la ré-identifier dans le jeu de données avec ces seules informations serait de 1 chance sur 43.
Choisir les variables quasi-identifiantes est un exercice difficile puisqu’en général, nous n’avons pas une idée exacte des données à la disposition des attaquants potentiels. Il faut donc définir un scénario théorique suffisamment réaliste pour s’assurer de protéger les données individuelles des risques de ré-identification les plus importants.
En choisissant le premier jeu de variables quasi-identifiantes (géographie, sexe et âge), on considère le jeu minimal de quasi-idenfiants. L’extrême inverse consisterait à considérer toutes les variable comme des quasi-identifiants. Dans le premier cas, on définit un scénario minimaliste, dans le second le scénario est maximaliste.
Dans notre jeu de données fictif sur l’emploi et le chômage, on pourrait définir
Selon ces trois scénarios, le niveau de risque de ré-identifcation des individus ne sera pas le même
Loading required package: tidyrggplot(risques_reident$r_graph |> ungroup()) +
geom_bar(aes(fill=p_cl, x = scenario, y = n),
stat = "identity", alpha = 0.6, color = "grey25", position = "dodge") +
scale_fill_brewer("Probabilité", type = "seq", palette = 7) +
labs(x="Scénario", y="Nb d'individus") +
ggtitle("Probabilité de ré-identification des individus selon le scénario") +
theme_minimal()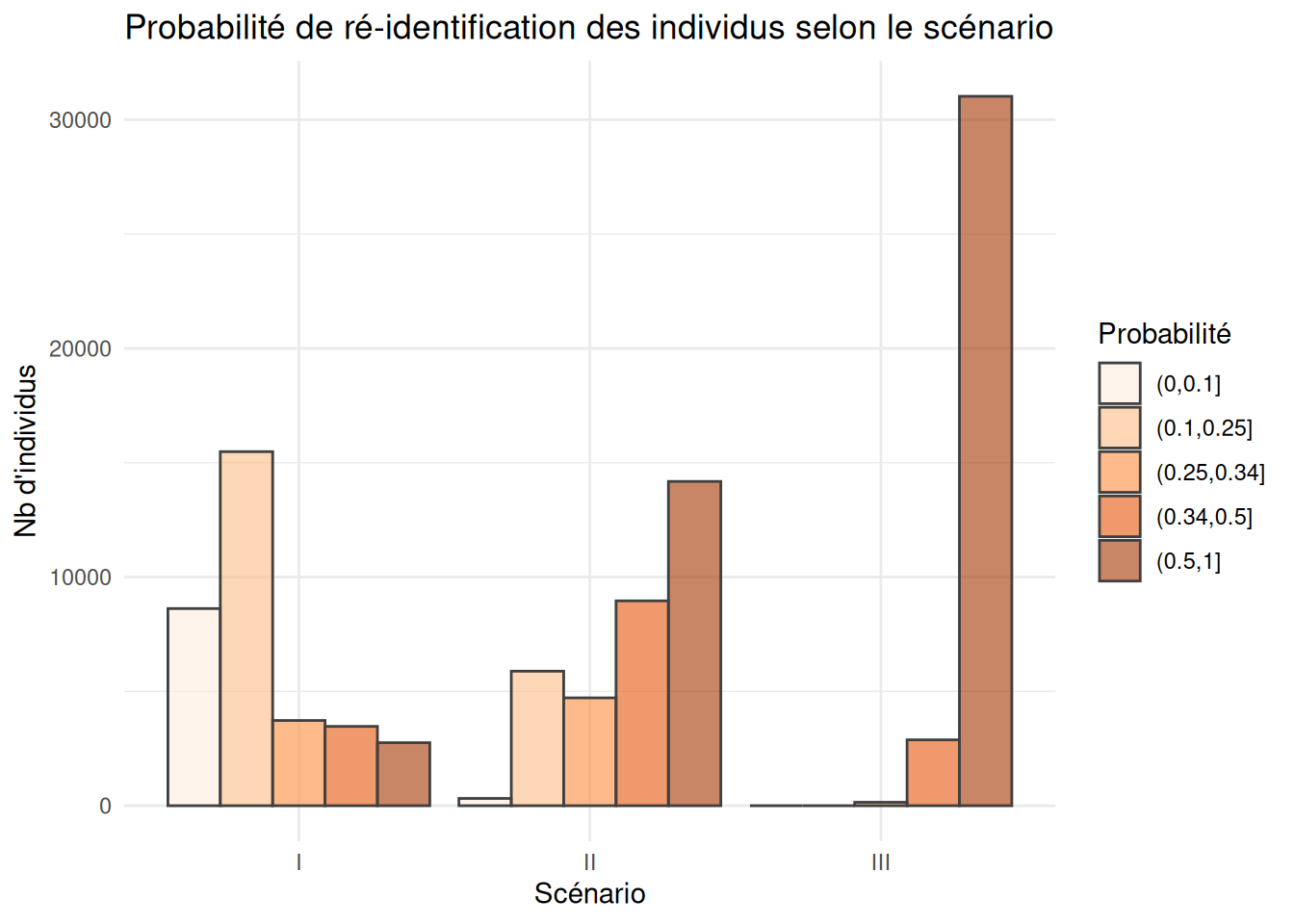
| scenario | p_moy | p_d1 | p_med | p_d9 | part_uniques |
|---|---|---|---|---|---|
| I | 0.508 | 0.125 | 0.333 | 1 | 8.090 |
| II | 0.802 | 0.333 | 1.000 | 1 | 41.641 |
| III | 0.977 | 1.000 | 1.000 | 1 | 91.102 |
Certaines variables ont un pouvoir de ré-identification très fort, en particulier :
la géographie (de résidence, de travail, d’implantation): plus elle est précise plus la ré-identification est aisée, d’autant plus que l’adresse est souvent par ailleurs une donnée très largement partagée par les individus et les entreprises.
l’âge est également très ré-identifiant puisqu’il est à la fois public avec la disponibilité de l’état-civil et concerne, pour certains âges avancés, peu d’individus. Ainsi, si la personne la plus âgée résidant en France est dans notre fichier, nous avons toutes les chances de la ré-identifier de façon certaine en ne connaissant que son âge.
Pour réduire le risque de ré-identification, il est souvent très efficace de choisir de diffuser des variables d’âge et de géographie agrégées.
Comparons, par exemple, trois scénarios alternatifs au scénario II présenté ci-dessus:
qi_vars_IIa <- c("REG", "DEP", "SEXE", "AGE", "DIP7")
qi_vars_IIb <- c("REG", "DEP", "ARR", "SEXE", "AGE6", "DIP7")
qi_vars_IIc <- c("REG", "DEP", "SEXE", "AGE6", "DIP7")
risques_reident2 <- list(
"II" = qi_vars_II,
"IIa" = qi_vars_IIa,
"IIb" = qi_vars_IIb,
"IIc" = qi_vars_IIc) |>
comparer_risque_reidentification(data = lfs_2023)| scenario | p_moy | p_d1 | p_med | p_d9 | part_uniques |
|---|---|---|---|---|---|
| II | 0.802 | 0.333 | 1.000 | 1.0 | 41.641 |
| IIa | 0.650 | 0.200 | 0.500 | 1.0 | 19.637 |
| IIb | 0.275 | 0.042 | 0.167 | 1.0 | 1.022 |
| IIc | 0.168 | 0.016 | 0.074 | 0.5 | 0.226 |
ggplot(risques_reident2$r_graph |> ungroup()) +
geom_bar(aes(fill=p_cl, x = scenario, y = n),
stat = "identity", alpha = 0.6, color = "grey25", position = "dodge") +
scale_fill_brewer("Probabilité", type = "seq", palette = 7) +
labs(x="Scénario", y="Nb d'individus") +
ggtitle("Probabilité de ré-identification des individus selon le scénario") +
theme_minimal()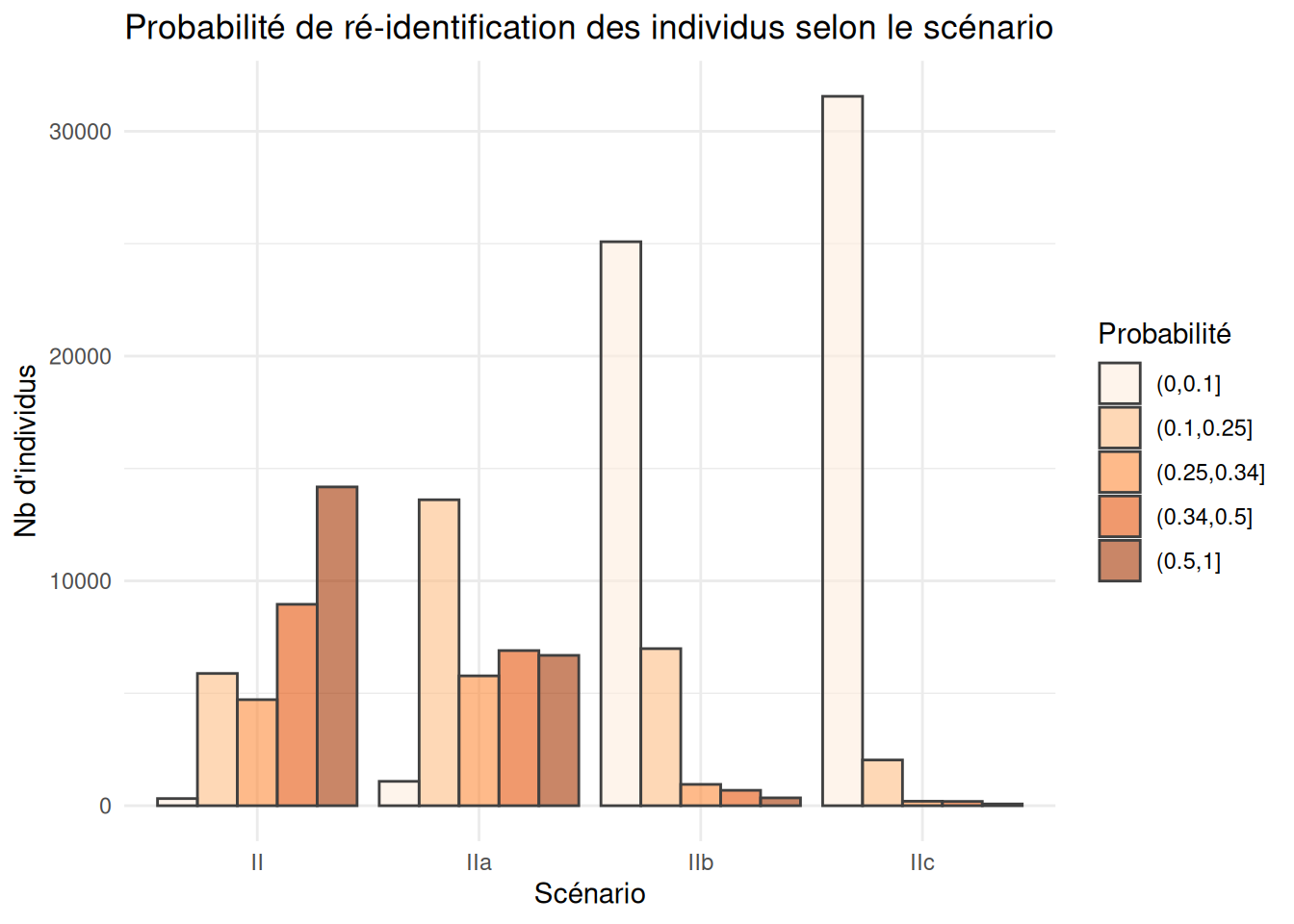
En réduisant le détail géographique, on a ici divisé par deux la part des uniques. Mais en passant à 6 tranches d’âges, celle-ci est divisée par 20!
Ainsi, les traitements les plus simples (recoder une variable) sont parfois les plus efficaces pour réduire massivement les risques individuels, même si cela ne les annihile pas tous.
sdcMicro
Le package sdcMicro permet de mesurer les risques de ré-identification et le niveau d’anonymité d’un jeu de données individuelles assez simplement.
Dans un premier temps, on initialise un objet de la classe sdcMicroObj en mentionnant uniquement le jeu de données et les variables considérées comme quasi-identfiantes.
La fonction crée un objet dans une classe S4. Les différents attributs de l’objet (on dit des slots) sont donc accessibles avec le symbole @.
Les attributs disponibles pour un tel objet sont les suivants:
[1] "origData" "keyVars" "pramVars"
[4] "numVars" "ghostVars" "weightVar"
[7] "hhId" "strataVar" "sensibleVar"
[10] "manipKeyVars" "manipPramVars" "manipNumVars"
[13] "manipGhostVars" "manipStrataVar" "originalRisk"
[16] "risk" "utility" "pram"
[19] "localSuppression" "options" "additionalResults"
[22] "set" "prev" "deletedVars" Lors de la création de l’objet, un certain nombre de métriques de risque ont été calculées. D’un point de vue global, la proportion d’individus à risque de ré-identification est une mesure calculée à partir des groupes constitués par les quasi-identifiants. Il s’agit du risque moyen qu’un individu de la base de donnée soit ré-identifié: \[ R = \frac{1}{n} \sum_i{ r_i }\], où \(r_i\) est le risque pour l’individu \(i\) d’être ré-identifié (voir plus bas pour plus de précision).
Le nombre de ré-identifications auxquelles on peut s’attendre en moyenne (risque global * n) est fourni par:
On peut également retrouver la part d’individus à risque au sens du \(k\)-anonymat:
Infos on 2/3-Anonymity:
Number of observations violating
- 2-anonymity: 77 (0.226%)
- 3-anonymity: 267 (0.784%)
- 5-anonymity: 825 (2.423%)
----------------------------------------------------------------------On observe en particulier que \(77\) individus sont uniques sur les clés utilisées (\(2\)-anonymity).
ou pour d’autres valeurs de \(k\), on peut faire, par exemple, pour \(k=10\):
On suppose que ACTEU est une variable sensible. Pour réduire le risque de divulgation d’attributs sur cette variable, on peut mesure la \(l\)-diversité du fichier et être particulier vigilant aux groupes de quasi-identifiants qui seraient constitués d’individus partageant la même catégorie.
--------------------------L-Diversity Measures -------------------------- Min. 1st Qu. Median Mean 3rd Qu. Max.
1.000 2.000 2.000 2.325 3.000 3.000 Calculons la part d’individus présents dans un groupe ne comptant qu’une seule des trois catégories:
En réalité, parmi les trois catégories de la variable, une seule est réellement sensible: il s’agit de la catégorie 2 correspondant aux personnes au chômage.
Vérifions le nombre d’individus réellement à risque de divulgation d’attributs sensibles:
risk fk Fk
[1,] 0.02777778 36 36
[2,] 0.04166667 24 24
[3,] 0.33333333 3 3
[4,] 0.03448276 29 29
[5,] 0.04000000 25 25
[6,] 0.02173913 46 46risk : risque individuel défini par \(\frac{1}{fk}\) si le fichier est une populationfk : nombre d’individus du fichier partageant les mêmes clés (croisements de quasi-identifiants)Fk : nombre d’individus dans la population partageant les mêmes clés (croisements de quasi-identifiants)Le risque de ré-identification est calculé différemment selon que l’on a affaire à une population ou à un échantillon.
Si le jeu de données étudié correspond à une population (fichier exhaustif du champ), alors \(fk = Fk = \sum_i{ 1(i \in k)}\), le nombre d’individus \(i\) partageant la clé \(k\).
Dans ce cas, le risque de ré-identification d’un individu est défini par \(r_k = 1/f_k = 1/F_k\) et correspond à la probabilité de ré-identifier l’individu correctement si on connaît ses caractéristiques \(k\) sur les variables quasi-identifiantes.
En se reportant aux premières lignes du tableau des risques présenté ci-dessous que la colonne risk est bien égale à 1/fk.
risk fk Fk
[1,] 0.02777778 36 36
[2,] 0.04166667 24 24
[3,] 0.33333333 3 3
[4,] 0.03448276 29 29
[5,] 0.04000000 25 25
[6,] 0.02173913 46 46Dans notre jeu de données, la distribution du risque individuel est la suivante (on multiplie par 100 pour l’interpréter comme le pourcentage de chances de correctement ré-identifier l’individu):
La grande partie des individus ont un risque inférieur à \(20\%\). On note qu’il y a des individus dont le risque est maximal, en revanche. Il s’agit d’individus uniques pour les clés que nous avons choisies:
Si, au contraire, il s’agit d’un échantillon, on distinguera:
où \(S\) désigne l’échantillon (le fichier) et \(w_i\) le poids de l’individu \(i \in S\).
En revanche, la colonne risk n’est pas calculée directement à partir des \(F_k\). En effet, un tel risque est jugé trop conservateur et conduit à surestimer le risque de ré-identification (Templ, Kowarik, et Meindl 2015; et Rinott et Shlomo 2006). En effet, les \(F_k\) sont en réalité des estimations. Une approche bayésienne est préférée (voir la présentation sur les mesures de risque pour plus de détails).
Le risque global moyen de ré-identification est alors (en %):
En prenant en compte les poids de l’échantillon, on a supposé en réalité le scénario d’attaque suivant:
Ainsi cette mesure de risque est pertinente si la connaissance de l’inclusion d’une personne dans l’échantillon est jugée trop peu réaliste.
En revanche, si l’inclusion d’une unité est certaine ou presque, il est préférable de mesurer ce risque au niveau de l’échantillon. C’est le cas par exemple pour les enquêtes entreprises qui incluent échantillonnent systématiquement les très grandes entreprises.
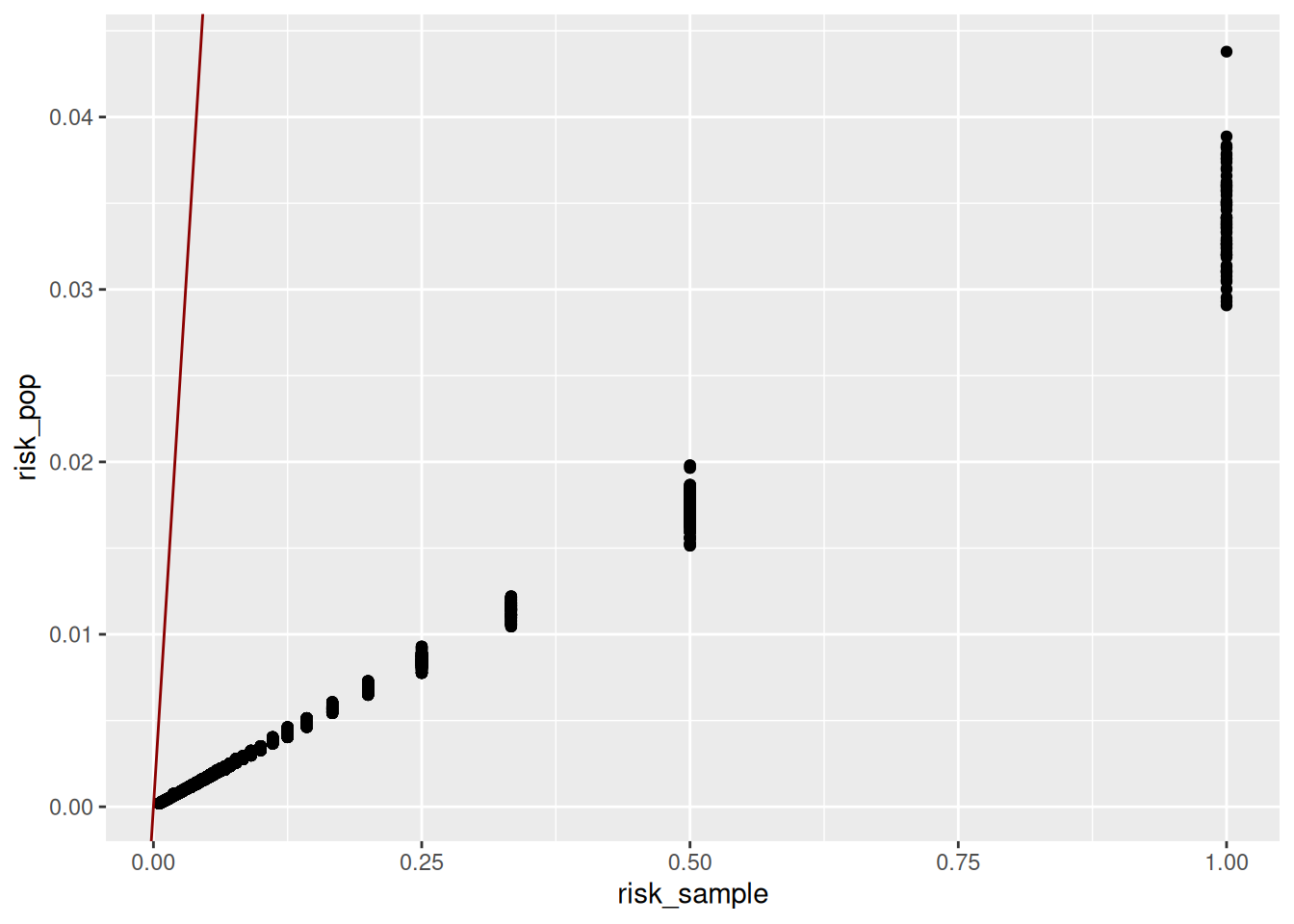
Au niveau individuel, le risque de ré-identification dans a population est également beaucoup plus faible:
risk fk Fk
[1,] 0.0009641090 36 1065.83365
[2,] 0.0014528593 24 717.18039
[3,] 0.0168594121 3 87.47107
[4,] 0.0011948446 29 865.78354
[5,] 0.0013632238 25 763.07839
[6,] 0.0007567189 46 1349.83893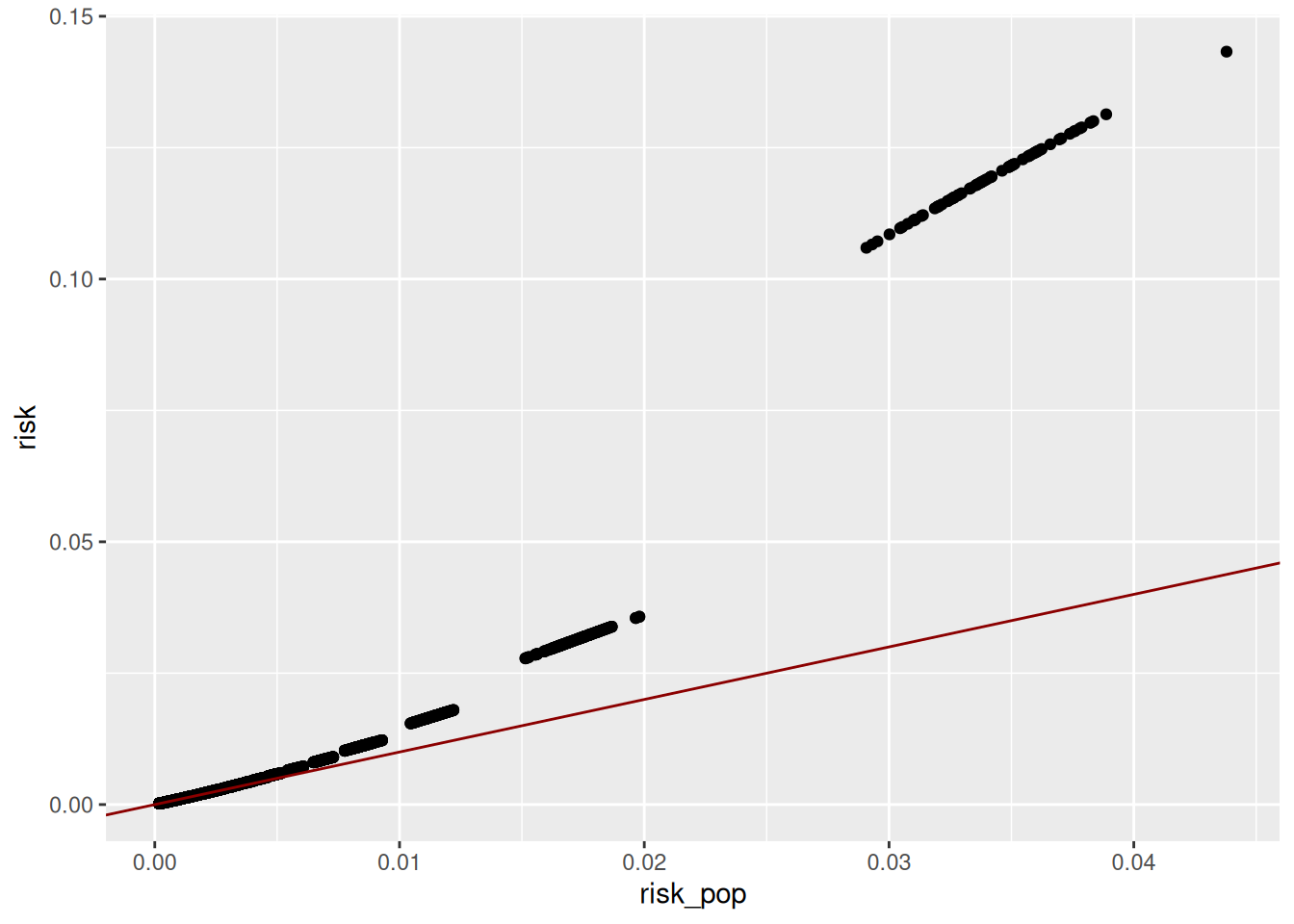
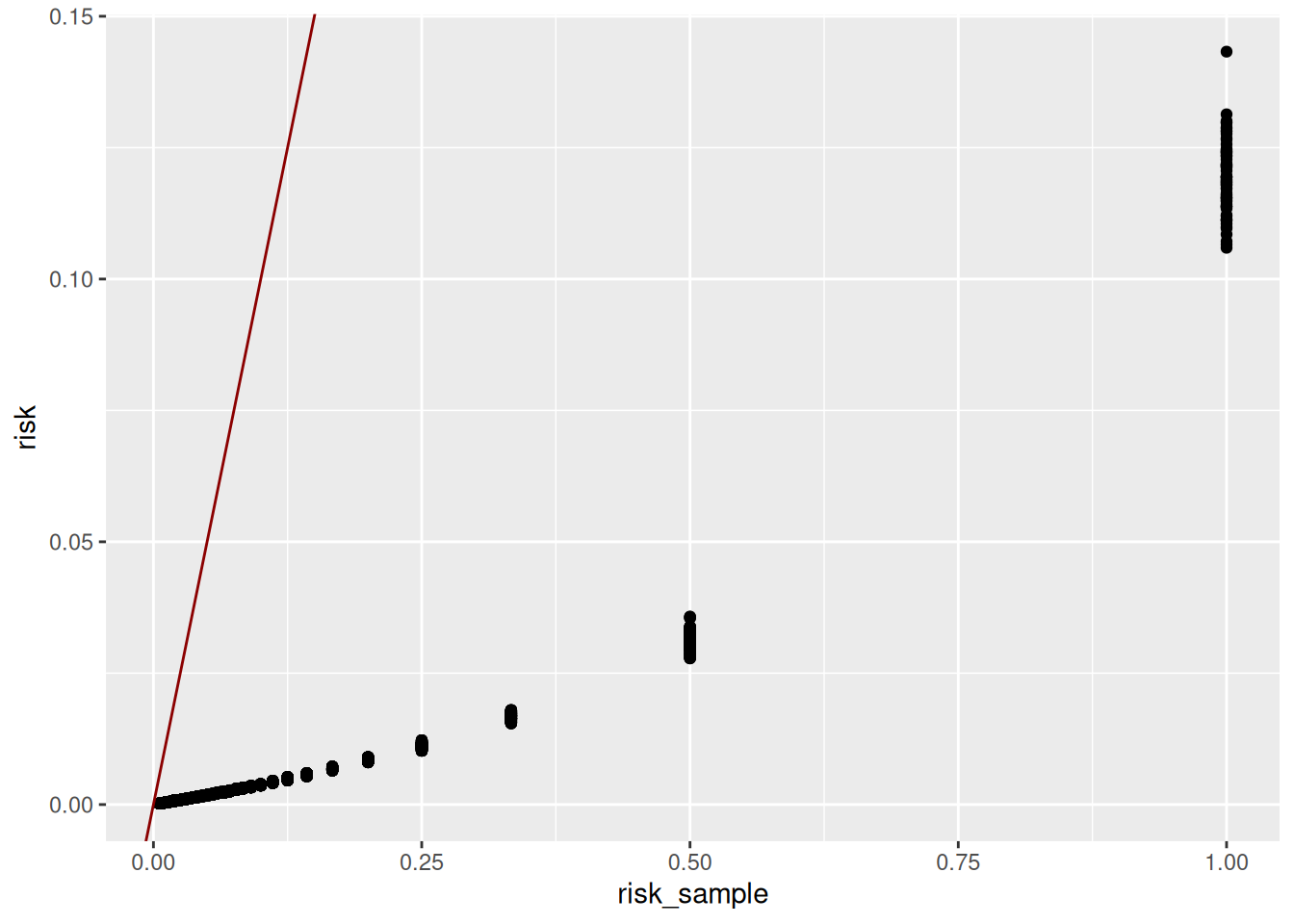
Regardons l’individu le plus à risque:
risk fk Fk
0.1432643 1.0000000 22.8362004 REG DEP ARR SEXE AGE AGE6 ACTEU DIP7 PCS1Q ANCCHOM HHID
<fctr> <fctr> <fctr> <fctr> <int> <fctr> <fctr> <fctr> <fctr> <fctr> <int>
1: 76 11 113 2 35 25 1 9 51 99 128
HH_TAILLE HH_AGE HH_DIP HH_PCS IS_CHOM poids
<fctr> <fctr> <fctr> <fctr> <int> <num>
1: 10 64 2 30 0 22.8362Quel est le risque de ré-identification dans le fichier public mis à disposition par l’Insee sur son site internet ?
Le fichier détail et sa documentation sont disponibles ici.
Téléchargeons le fichier:
La documentation des variables:
Quelles variables du jeu pourraient servir à la ré-identification des individus enquêtés ?
Imaginons que l’attaquant dispose d’un fichier client très riche sur une très grande partie de la population françasise. Dans un tel scénario, nous sommes amenés à avoir une définition extensive des variables quasi-identifiantes:
qi_1 <- c(
"SEXE",
"AGE6", # la classe d'âge (6 catégories)
"ACTEU", # le statut d'activité de la personne
"DIP7", # le niveau de diplôme
"METRODOM", # le lieu de résidence Hexagone ou Territoires Ultra-Marins
"APCS1", # Catégorie socio-professionnelle du dernier emploi (6 classes)
"STATUT", # Statut dans l'emploi (salarié, indépendant)
"STCOMM2020", #Statut de la commune dans l'unité urbaine (information publique si on suppose que l'attauqant dispose des adresses des personnes)
"SALTYP", # Nature du contrat (Fonctionnaire, CDI, CDD, etc.)
"PCS1Q" # Catégorie socio-professionnelle de l'emploi principal
)Déterminons le niveau de risque de ré-identification:
Le niveau d’anonyité de l’échantillon:
Il existe des uniques dans l’échantillon (1818).
Le risque de ré-identification évaluée par la mesure globale fournie par sdcMicro est évaluée à 0.00078, soit moins de 0.1% de risque de ré-identification, ce qui est très faible.
Si la mesure globale est très faible, est-ce qu’il demeure des cas individuels problématiques. En particulier: quel est le risque de ré-identification des uniques de l’échantillon ?
Dans ce scénario d’attaque, supposons que toute attaque avec une chance de ré-identification supérieure à 50% est problématique:
Il reste 11 individus, dont 1 avec un risque quasi certain d’être ré-identifié dans le scénario que nous nous sommes fixés.
Quelles sont les limites du scénario envisagé ci-dessus ?
---
title: Les mesures du risque de divulgation
href: pratique/fiches/mesurer-risque.html
code-block-bg: true
code-block-border-left: "#bf9aff"
code-fold: show
---
# Les packages
```{r}
#| eval: false
#| echo: false
setwd("./pratique/fiches")
```
```{r}
#| echo: true
#| message: false
#| output: false
library(readr)
library(purrr)
library(ggplot2)
library(dplyr)
library(sdcMicro)
```
## Les données
```{r}
#| echo: true
#| message: false
source("../R/fun_risque.R")
```
```{r}
source("../R/fun_import_data.R")
lfs_2023 <- import_lfs()
```
```{r}
head(lfs_2023)
```
## Les différents types de variables
Dans un jeu de données, on distingue trois grands types de variables:
- les *quasi-identifiants*: un ensemble de variables dont on suppose qu'un
attaquant est susceptible de les avoir déjà à sa disposition.
- les *variables sensibles*: les variables portant sur des thématiques
sensibles au sens de la Loi Informatique et Libertés
(religion, opinion, orientation sexuelle, etc.), mais on peut aussi y inclure
des variables dont la connaissance est susceptible de porter préjudice
à la personne (par exemple le salaire, le fait d'avoir une maladie, le fait
d'être au chômage, etc.).
- les *variables ni identifiantes ni sensibles*: celles qui a priori ne
posent pas de problème spécifique en terme de confidentialité.
## Le risque de ré-identification et le rôle des quasi-identifiants
Ainsi, le premier type de variables engendre un risque de divulgation d'information
confidentielle par la possibilité pour l'attaquant de ré-identifier des individus.
En effet, si un ataquant dispose d'un fichier nomminatif - un fichier client par
exemple - contenant des variables communes avec le jeu de données qu'on s'apprête
à publier, il est alors en mesure d'apparier les deux et être en capacité de
ré-identifier des individus si ceux-ci se trouvent avoir des caractéristiques
peu fréquentes.
### Un premier exemple
Prenons une liste très restreinte de quasi-identifiants: la géographie de résidence,
le sexe et l'âge de l'individu. Ces informations sont disponibles par de
nombreuses entreprises auprès desquelles nous souscrivons des services
(banque, assurance, téléphonie, etc.).
En dénombrant les individus de chaque croisement entre les variables quasi-identifiantes,
on peut détecter :
- le **niveau d'anonymité du fichier** au sens du **k-anonymat**: ici notre fichier est
1-anonyme puisqu'il contient de nombreux individus uniques dans leur catégorie.
- la détection des croisements et des **individus les plus à risque**:
> Moins il y a d'individus dans un groupe, plus la probabilité de ré-identification
par l'attaquant est forte. Dans le cas d'un groupe unique, la ré-identification
est même certaine.
```{r}
qi_vars_I <- c("REG","DEP","ARR", "SEXE", "AGE")
freq_qi_vars <- lfs_2023 |> count(across(all_of(qi_vars_I)))
freq_qi_vars |> arrange(n) |> head()
freq_qi_vars |> arrange(-n) |> head()
```
Ainsi, si une entreprise de notre contrée imaginaire dispose d'un fichier sur
tout ou partie de la population en âge de travailler (par exemple un opérateur
téléphonique), il pourra ré-identifier sans peine les individus uniques du jeu
de données qui seraient présents dans son fchier.
La **capacité d'un attaquant à pouvoir ré-identifier un individu** dépend du
nombre d'individus du jeu de données qui partagent les mêmes caractéristiques
sur les variables quasi-identifiantes.
Par exemple, si Thérèse est une femme de 97 ans résidant dans l'arrondissement `751`,
alors le jeu de données permet de la ré-identifier de façon certaine, puisqu'elle
serait la seule dans ce cas.
Au contraire, si Thérèse est une femme de 52 ans résidant dans le même arrondissement,
alors la probabilité de la ré-identifier dans le jeu de données
avec ces seules informations serait de 1 chance sur
`r freq_qi_vars |> filter(ARR == "751", SEXE == 2, AGE == 52) |> pull(n)`.
<!-- ```{r} -->
<!-- freq_qi_vars <- freq_qi_vars |> -->
<!-- mutate(p = 1/n) |> -->
<!-- mutate(p_cl = cut(p, breaks = c(0,0.1,0.25,0.34,0.5,1))) -->
<!-- ``` -->
<!-- ```{r} -->
<!-- #| code-fold: true -->
<!-- ggplot(freq_qi_vars) + -->
<!-- geom_bar(aes(x=p_cl), fill = "forestgreen", alpha = 0.6, color = "snow") + -->
<!-- labs(x="Probabilité d'être ré-identifié", y="Nb d'individus") + -->
<!-- ggtitle("Probabilité de ré-identification des individus") + -->
<!-- theme_minimal() -->
<!-- ``` -->
### Le choix des variables quasi-identifiantes
Choisir les variables quasi-identifiantes est un exercice difficile puisqu'en
général, nous n'avons pas une idée exacte des données à la disposition
des attaquants potentiels. Il faut donc définir un scénario théorique suffisamment
réaliste pour s'assurer de **protéger** les données individuelles
des risques de ré-identification les plus importants.
En choisissant le premier jeu de variables quasi-identifiantes (géographie, sexe et âge),
on considère le jeu minimal de quasi-idenfiants. L'extrême inverse consisterait
à considérer toutes les variable comme des quasi-identifiants. Dans le premier
cas, on définit un scénario minimaliste, dans le second le scénario est maximaliste.
Dans notre jeu de données fictif sur l'emploi et le chômage, on pourrait définir
- un scénario minimaliste: l'attaquant ne dispose que de la géographie, du sexe et de l'âge de ses clients
- un scénario intermédiaire: l'attaquant dispose en plus d'informations sur son niveau de diplôme
- un scénario maximaliste: l'attaquant dispose en réalité de toutes les informations sur les individus sauf de son ancienneté au chômage.
Selon ces trois scénarios, le niveau de risque de ré-identifcation des individus ne sera pas le même
```{r}
qi_vars_II <- c(qi_vars_I, "DIP7")
qi_vars_III <- c(names(lfs_2023)[!names(lfs_2023) %in% c("ANCCHOM")])
risques_reident <-
list("I" = qi_vars_I,
"II" = qi_vars_II,
"III" = qi_vars_III) |>
comparer_risque_reidentification(data = lfs_2023)
```
```{r}
#| cold-fold: true
ggplot(risques_reident$r_graph |> ungroup()) +
geom_bar(aes(fill=p_cl, x = scenario, y = n),
stat = "identity", alpha = 0.6, color = "grey25", position = "dodge") +
scale_fill_brewer("Probabilité", type = "seq", palette = 7) +
labs(x="Scénario", y="Nb d'individus") +
ggtitle("Probabilité de ré-identification des individus selon le scénario") +
theme_minimal()
```
```{r}
#| code-fold: true
risques_reident$r_stats |>
knitr::kable(
caption = "Risque de ré-identification des individus en fonction du scénario",
digits = 3
)
```
::: {.callout-warning}
### Des variables très efficaces pour la ré-identification
Certaines variables ont un pouvoir de ré-identification très fort, en particulier :
- la **géographie** (de résidence, de travail, d'implantation): plus elle est précise
plus la ré-identification est aisée, d'autant plus que l'adresse est souvent par
ailleurs une donnée très largement partagée par les individus et les entreprises.
- l'**âge** est également très ré-identifiant puisqu'il est à la fois public avec
la disponibilité de l'état-civil et concerne, pour certains âges avancés, peu
d'individus. Ainsi, si la personne la plus âgée résidant en France est dans notre
fichier, nous avons toutes les chances de la ré-identifier de façon certaine
en ne connaissant que son âge.
Pour réduire le risque de ré-identification, il est souvent très efficace de
choisir de diffuser des variables d'âge et de géographie agrégées.
Comparons, par exemple, trois scénarios alternatifs au `scénario II` présenté
ci-dessus:
- **scénario II-a**: le lieu de résidence n'est plus diffusé à l'arrondisement mais au département.
- **scénario II-b**: l'âge détaillé est remplacé par 5 tranches d'âges.
- **scénario II-c**: combinaison des deux scénarios ci-dessus.
```{r}
qi_vars_IIa <- c("REG", "DEP", "SEXE", "AGE", "DIP7")
qi_vars_IIb <- c("REG", "DEP", "ARR", "SEXE", "AGE6", "DIP7")
qi_vars_IIc <- c("REG", "DEP", "SEXE", "AGE6", "DIP7")
risques_reident2 <- list(
"II" = qi_vars_II,
"IIa" = qi_vars_IIa,
"IIb" = qi_vars_IIb,
"IIc" = qi_vars_IIc) |>
comparer_risque_reidentification(data = lfs_2023)
```
```{r}
#| code-fold: true
risques_reident2$r_stats |>
knitr::kable(
caption = "Risque de ré-identification des individus en fonction du scénario",
digits = 3
)
```
```{r}
#| cold-fold: true
ggplot(risques_reident2$r_graph |> ungroup()) +
geom_bar(aes(fill=p_cl, x = scenario, y = n),
stat = "identity", alpha = 0.6, color = "grey25", position = "dodge") +
scale_fill_brewer("Probabilité", type = "seq", palette = 7) +
labs(x="Scénario", y="Nb d'individus") +
ggtitle("Probabilité de ré-identification des individus selon le scénario") +
theme_minimal()
```
En réduisant le détail géographique, on a ici divisé par deux la part des uniques.
Mais en passant à 6 tranches d'âges, celle-ci est divisée par 20!
Ainsi, les traitements les plus simples (recoder une variable) sont parfois
les plus efficaces pour réduire massivement les risques individuels, même si
cela ne les annihile pas tous.
:::
### Avec le package `sdcMicro`
Le package `sdcMicro` permet de mesurer les risques de ré-identification et le
niveau d'anonymité d'un jeu de données individuelles assez simplement.
Dans un premier temps, on initialise un objet de la classe `sdcMicroObj` en
mentionnant uniquement le jeu de données et les variables considérées
comme quasi-identfiantes.
```{r}
lfs_sdc <- sdcMicro::createSdcObj(
lfs_2023,
keyVars = qi_vars_IIc
)
```
La fonction crée un objet dans une classe `S4`. Les différents attributs de l'objet (on dit des `slots`) sont donc accessibles avec le symbole `@`.
Les attributs disponibles pour un tel objet sont les suivants:
```{r}
slotNames(lfs_sdc)
```
Lors de la création de l'objet, un certain nombre de métriques de risque ont été calculées. D'un point de vue global, la proportion d'individus à risque de ré-identification est une mesure calculée à partir des groupes constitués par les quasi-identifiants. Il s'agit du risque moyen qu'un individu de la base de donnée soit ré-identifié: $$ R = \frac{1}{n} \sum_i{ r_i }$$, où $r_i$ est le risque pour l'individu $i$ d'être ré-identifié (voir plus bas pour plus de précision).
```{r}
lfs_sdc@risk$global$risk * 100
```
Le nombre de ré-identifications auxquelles on peut s'attendre en moyenne (risque global * n) est fourni par:
```{r}
lfs_sdc@risk$global$risk_ER
```
On peut également retrouver la part d'individus à risque au sens du $k$-anonymat:
```{r}
print(lfs_sdc, 'kAnon')
```
On observe en particulier que $77$ individus sont uniques sur les clés utilisées ($2$-anonymity).
ou pour d'autres valeurs de $k$, on peut faire, par exemple, pour $k=10$:
```{r}
mean(lfs_sdc@risk$individual[,"fk"] < 10)*100
```
## Le risque de divulgation d'attributs sensibles
On suppose que `ACTEU` est une variable sensible. Pour réduire
le risque de divulgation d'attributs sur cette variable, on peut
mesure la $l$-diversité du fichier et être particulier vigilant
aux groupes de quasi-identifiants qui seraient constitués
d'individus partageant la même catégorie.
```{r}
lfs_sdc <- ldiversity(obj = lfs_sdc, ldiv_index = c("ACTEU"), missing = NA)
lfs_sdc@risk$ldiversity
```
Calculons la part d'individus présents dans un groupe ne comptant qu'une seule des trois catégories:
```{r}
mean(lfs_sdc@risk$ldiversity[,"ACTEU_Distinct_Ldiversity"]==1)*100
```
En réalité, parmi les trois catégories de la variable, une seule est réellement sensible: il s'agit de la catégorie `2` correspondant aux personnes au chômage.
Vérifions le nombre d'individus réellement à risque de divulgation d'attributs sensibles:
```{r}
indiv_1diverses <- which(lfs_sdc@risk$ldiversity[,"ACTEU_Distinct_Ldiversity"]==1)
lfs_2023|>
slice(indiv_1diverses)|>
filter(ACTEU == 2)|>
nrow()
```
## Les mesures du risque individuel
```{r}
head(lfs_sdc@risk$individual)
```
- `risk` : risque individuel défini par $\frac{1}{fk}$ si le fichier est une population
- `fk` : nombre d'individus du fichier partageant les mêmes clés (croisements de quasi-identifiants)
- `Fk` : nombre d'individus dans la population partageant les mêmes clés (croisements de quasi-identifiants)
Le risque de ré-identification est calculé différemment selon que l'on a affaire à une population ou à un échantillon.
::: {.callout-note}
### Echantillon et Population
#### Population
Si le jeu de données étudié correspond à une population (fichier exhaustif du champ),
alors $fk = Fk = \sum_i{ 1(i \in k)}$, le nombre d'individus $i$ partageant la clé $k$.
Dans ce cas, le risque de ré-identification d'un individu est défini par $r_k = 1/f_k = 1/F_k$ et correspond à la probabilité de ré-identifier l'individu correctement si on connaît ses caractéristiques $k$ sur les variables quasi-identifiantes.
En se reportant aux premières lignes du tableau des risques présenté ci-dessous que la colonne `risk` est bien égale à `1/fk`.
```{r}
head(lfs_sdc@risk$individual)
```
Dans notre jeu de données, la distribution du risque individuel est la suivante (on multiplie par 100 pour l'interpréter comme le pourcentage de chances de correctement ré-identifier l'individu):
```{r}
hist(lfs_sdc@risk$individual[,"risk"]*100)
```
La grande partie des individus ont un risque inférieur à $20\%$. On note qu'il y a des individus dont le risque est maximal, en revanche. Il s'agit d'individus uniques pour les clés que nous avons choisies:
```{r}
sum(lfs_sdc@risk$individual[,"risk"] == 1)
```
#### Echantillon
Si, au contraire, il s'agit d'un échantillon, on distinguera:
- $fk = \sum_{i \in S}{ 1(i \in k)}$
- $Fk = \sum_{i \in S}{ w_i \times 1(i \in k)}$
où $S$ désigne l'échantillon (le fichier) et $w_i$ le poids de l'individu
$i \in S$.
En revanche, la colonne `risk` n'est pas calculée directement à partir des $F_k$. En effet, un tel risque est jugé trop conservateur et conduit à surestimer le risque de ré-identification [@templ_statistical_2015; et @Rinott_Shlomo_2006]. En effet, les $F_k$ sont en réalité des estimations. Une approche bayésienne est préférée
(voir [la présentation sur les mesures de risque](theorie/supports/arbitrer-risque-utilite.html) pour plus de détails).
```{r}
set.seed(14789)
N = 1e6
n = nrow(lfs_2023)
w = N/n + rnorm(n-1, -2/(n-1), 2)
w = c(w, N-sum(w))
lfs_samp <- lfs_2023 |>
mutate(poids = sample(w, n, replace=TRUE))
```
```{r}
lfs_sdc_samp <- sdcMicro::createSdcObj(
lfs_samp,
keyVars = qi_vars_IIc,
weightVar = "poids"
)
```
Le risque global moyen de ré-identification est alors (en %):
```{r}
lfs_sdc_samp@risk$global$risk * 100
```
En prenant en compte les poids de l'échantillon, on a supposé en réalité le scénario d'attaque suivant:
- l'attaquant cherche à ré-identifier des personnes de l'échantillon à partir d'informations qu'il dispose sur la population
- mais il ne sait pas si un individu a été enquêté ou non.
Ainsi cette mesure de risque est pertinente si la connaissance de l'inclusion d'une personne dans l'échantillon est jugée trop peu réaliste.
En revanche, si l'inclusion d'une unité est certaine ou presque, il est préférable de mesurer ce risque au niveau de l'échantillon. C'est le cas par exemple pour les enquêtes entreprises qui incluent échantillonnent systématiquement les très grandes entreprises.
Au niveau individuel, le risque de ré-identification dans a population est également beaucoup plus faible:
```{r}
head(lfs_sdc_samp@risk$individual)
```
```{r}
hist(lfs_sdc_samp@risk$individual[,"risk"]*100)
```
```{r}
all_risks <- lfs_sdc_samp@risk$individual |>
as.data.frame() |>
mutate(risk_sample = 1/fk, risk_pop=1/Fk)
```
```{r}
all_risks |>
ggplot(aes(x=risk_pop, y=risk)) +
geom_point() +
geom_abline(slope = 1, intercept = 0, color = 'darkred')
```
```{r}
all_risks |>
ggplot(aes(x=risk_sample, y=risk)) +
geom_point() +
geom_abline(slope = 1, intercept = 0, color = 'darkred')
```
```{r}
all_risks |>
ggplot(aes(x=risk_sample, y=risk_pop)) +
geom_point() +
geom_abline(slope = 1, intercept = 0, color = 'darkred')
```
Regardons l'individu le plus à risque:
```{r}
max_risk <- which.max(lfs_sdc_samp@risk$individual[,"risk"])
lfs_sdc_samp@risk$individual[max_risk,]
lfs_samp |> slice(max_risk)
```
:::
## Exercice pratique
Quel est le risque de ré-identification dans le fichier public mis à disposition par l'Insee sur son site internet ?
Le fichier détail et sa documentation sont disponibles [ici](https://www.insee.fr/fr/statistiques/6654604).
Téléchargeons le fichier:
```{r}
#| eval: false
options(timeout = 6000)
download.file(
destfile = "lfs_micro_fr_2023.zip",
url = "https://www.insee.fr/fr/statistiques/fichier/8241122/FD_csv_EEC23.zip"
)
unzip(zipfile = "lfs_micro_fr_2023.zip", exdir = ".")
```
```{r}
#| eval: false
puf_lfs = data.table::fread(
"FD_csv_EEC23.csv"
) %>%
# On conserve uniquement les ménages dont la personne est âgée entre 15 et 89 ans
filter(CHAMP_M_15_89 == 1) %>%
select(-CHAMP_M_15_89)
```
```{r}
#| eval: false
dim(puf_lfs)
```
La documentation des variables:
```{r}
#| eval: false
doc_lfs <- data.table::fread(
"Varmod_EEC_2023.csv"
) |>
select(COD_VAR, LIB_VAR) |>
unique()|>
as.data.frame()
doc_lfs
```
Quelles variables du jeu pourraient servir à la ré-identification des individus enquêtés ?
Imaginons que l'attaquant dispose d'un fichier client très riche sur une très grande partie de la population françasise. Dans un tel scénario, nous sommes amenés à avoir une définition extensive des variables quasi-identifiantes:
```{r}
#| eval: false
qi_1 <- c(
"SEXE",
"AGE6", # la classe d'âge (6 catégories)
"ACTEU", # le statut d'activité de la personne
"DIP7", # le niveau de diplôme
"METRODOM", # le lieu de résidence Hexagone ou Territoires Ultra-Marins
"APCS1", # Catégorie socio-professionnelle du dernier emploi (6 classes)
"STATUT", # Statut dans l'emploi (salarié, indépendant)
"STCOMM2020", #Statut de la commune dans l'unité urbaine (information publique si on suppose que l'attauqant dispose des adresses des personnes)
"SALTYP", # Nature du contrat (Fonctionnaire, CDI, CDD, etc.)
"PCS1Q" # Catégorie socio-professionnelle de l'emploi principal
)
```
Déterminons le niveau de risque de ré-identification:
```{r}
#| eval: false
puf_sdc <- sdcMicro::createSdcObj(
puf_lfs,
keyVars = qi_1,
weightVar = "EXTRIAN"
)
```
Le niveau d'anonyité de l'échantillon:
```{r}
#| eval: false
print(puf_sdc, 'kAnon')
```
Il existe des uniques dans l'échantillon (1818).
Le risque de ré-identification évaluée par la mesure globale fournie par `sdcMicro` est évaluée à 0.00078, soit moins de 0.1% de risque de ré-identification, ce qui est très faible.
```{r}
#| eval: false
puf_sdc@risk$global$risk
```
Si la mesure globale est très faible, est-ce qu'il demeure des cas individuels problématiques. En particulier: quel est le risque de ré-identification des uniques de l'échantillon ?
```{r}
#| eval: false
risk_unique_echantillon <- puf_sdc@risk$individual |>
as.data.frame()|>
filter(fk == 1)
risk_unique_echantillon |>
pull(risk) |>
quantile(probs=seq(0,1,.1))
```
Dans ce scénario d'attaque, supposons que toute attaque avec une chance de ré-identification supérieure à 50% est problématique:
```{r}
#| eval: false
risk_unique_echantillon |>
filter(risk > 0.5) |>
arrange(-risk)
```
Il reste 11 individus, dont 1 avec un risque quasi certain d'être ré-identifié dans le scénario que nous nous sommes fixés.
```{r}
#| eval: false
max_risk_puf <- which.max(puf_sdc@risk$individual[,"risk"])
puf_sdc@risk$individual[max_risk,]
puf_lfs |> slice(max_risk) |> select(all_of(qi_1))
```
### Exercice
Quelles sont les limites du scénario envisagé ci-dessus ?
### References
::: {#refs}
:::